Angle
between vectors
This
article describes how to calculate
the angle between vectors, the angle
between
each vector and axis, and the magnitude of each vector. The vectors are
given
in three-dimensional space. The code and examples were developed in
Matlab
code.
| |
We are going to enter the tip of the
vectors assuming that
they both start at the origin
point (0, 0, 0). For example, to enter vector V1 that goes from (0, 0,
0) to (3, 4, 7) we have to enter just the last point, in a row array in
Matlab, like this:
v1 = [3 4 7]
We
now
develop a function to calculate the values, and another function to
display
those values, in order to be
|
able to call those scripts whenever we
need them
and avoid retyping instructions for every couple of vectors that we use.
The
script to find relevant values is:
function [m, a]
= ab2v(v1, v2)
%
Magnitude of vector is its norm
m(1) =
norm(v1);
m(2) =
norm(v2);
%
Min. angles from vector 1 to axes
a(1 : 3)
= acosd(v1 / m(1));
%
Min. angles from vector 2 to axes
a(4 : 6)
= acosd(v2 / m(2));
%
Dot product dot(v1, v2) equals sum(v1 .* v2)
a(7) =
acosd(dot(v1, v2) / m(1) / m(2));
The
m-file to display and format those values is:
function
display_angles(m, a)
disp(' ')
disp(['Angle
between vectors: '
num2str(a(7))])
disp(' ')
disp('Vector
1')
disp(['Magnitude
:' num2str(m(1))])
disp(['Min.
angle with x-axis: '
num2str(a(1))])
disp(['Min.
angle with y-axis: '
num2str(a(2))])
disp(['Min.
angle with z-axis: '
num2str(a(3))])
disp(' ')
disp('Vector
2')
disp(['Magnitude
:'
num2str(m(2))])
disp(['Min.
angle with x-axis: '
num2str(a(4))])
disp(['Min.
angle with y-axis: '
num2str(a(5))])
disp(['Min.
angle with z-axis: '
num2str(a(6))])
Built-in function ‘num2str’ converts
numbers to strings, in
order to concatenate them to other strings and improve the formatting
previously to display the results on screen.
Example 1:
Find the angle between a
diagonal of a cube and a diagonal
of one of its faces. The cube measures 5x5x5 units.
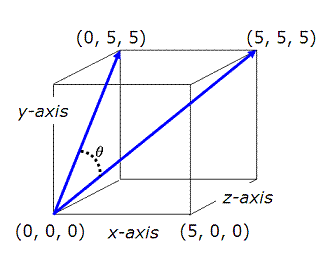
We finally create a third
Matlab script, to try our
functions above and to drive them effortlessly. This gives us an easy
way to
handle all the examples that we’d like to test...
clc;
clear; close all; format compact
v1 = [0
5 5]
v2 = [5
5 5]
[m, a] =
ab2v(v1, v2);
display_angles(m,
a)
The on-screen
result is:
Angle
between vectors: 35.2644
Vector
1
Magnitude
:7.0711
Min.
angle with x-axis: 90
Min.
angle with y-axis: 45
Min.
angle with z-axis: 45
Vector
2
Magnitude
:8.6603
Min.
angle with x-axis: 54.7356
Min.
angle with y-axis: 54.7356
Min.
angle with z-axis: 54.7356
Example
2:
Find
out the angle between vectors (1, 0, 0) and (1, 1, 0).
It’s
nice to have this case as an example, because we can figure it out from
the
beginning, right?
We run
our driver:
clc;
clear; close all; format compact
v1 = [1
0 0]
v2 = [1
1 0]
[m, a] =
ab2v(v1, v2);
display_angles(m,
a)
And find
the solution:
Angle
between vectors: 45
Vector
1
Magnitude
:1
Min.
angle with x-axis: 0
Min.
angle with y-axis: 90
Min.
angle with z-axis: 90
Vector
2
Magnitude
:1.4142
Min.
angle with x-axis: 45
Min.
angle with y-axis: 45
Min.
angle with z-axis: 90
From
'Angle
between Vectors' to home
From 'Angle
between Vectors' to 'Matlab Programming'


|




