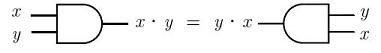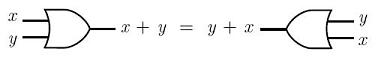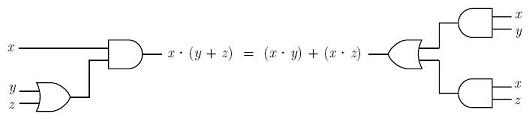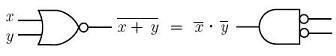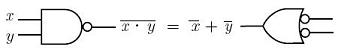 |
Axioms -
Laws of Boolean Algebra
Boolean
algebra is the algebra of propositions. Propositions
are denoted by letters, such as A, B, x or y, etc.
|
|
In the following axioms
and theorems (laws of boolean algebra), the '+'
or 'V' signs
represent a logical OR (or
conjunction),
the '.' or '^' signs represent a
logical
AND (or
disjunction),
and '¬' or '~' represent a logical NOT ( or negation).
Every proposition has two possible values: 1 (or T) when the
proposition is true
and 0 (or F) when the
proposition is false.
|
The negation
of A is written as ¬A
(or ~A) and
read as 'not A'.
If A is true then ¬A is false. Conversely, if A is false then ¬A is
true.
Basic Laws of Boolean Algebra
| Descript. |
OR
form |
AND
form |
Other way to express it: |
| Axiom |
x+0
= x |
x.1
= x |
A
V F = A
A ^ T = A |
| Commutative |
x+y
= y+x |
x.y
= y.x |
A
V B = B V A
A ^ B = B ^ A |
| Distributive |
x.(y+z)
= (x.y)+(x.z) |
x+y.z
= (x+y).(x+z) |
A
^ (B V C) = (A ^ B) V (A ^ C)
A V B ^ C = (A V B) ^ (A V C) |
| Axiom |
x+¬x
= 1 |
x.¬x
= 0 |
A
V ¬A = T
A ^ ¬A = F |
| Theorem |
x+x
= x |
x.x
= x |
A
V A = A
A ^ A = A |
| Theorem |
x+1
= 1 |
x.0
= 0 |
A
V T = T
A ^ F = F |
| Theorem |
¬¬x
= x |
|
¬(¬A)
= A |
| Associativity |
x+(y+z)
= (x+y)+z |
x.(y.z)
= (x.y).z |
A
V (B V C) = (A V B) V C
A ^ (B ^ C) = (A ^ B) ^ C |
| Absorption |
x+x.y
= x |
x.(x+y)
= x |
A
V A ^ B = A
A ^ (A V B) = A |
| DeMorgan's
laws |
x+y
= ¬(¬x.¬y) |
x.y
= ¬(¬x+¬y) |
A
V B = ¬(¬A ^ ¬B)
A ^ B = ¬(¬A V ¬B) |
Using logical gates, the commutative
property for a logical
AND is:
The commutative property for a logical
OR, is:
Using electronic gates, the distributive property is:
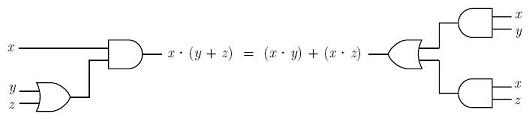
The De Morgan's laws
can transform logical ORs into logical ANDs (negations are necessary)
and can electronically be described this way:
or
From
'Axioms' to home
From
'Axioms' to 'Boolean Algebra'
|
|
