Binary to hexadecimal numbers:  two solutions in Matlab 

To convert a value from binary to hexadecimal, we first need to know what a hexadecimal number is. 

A major numbering system used in digital systems is the hexadecimal system, also named base 16. In this system, the numbers are counted from 0 to 9 and, since in base 16 we need 16 different symbols, decimal numbers 10 through 15 are represented by letters A through F, respectively. So we go from 0 to F.  

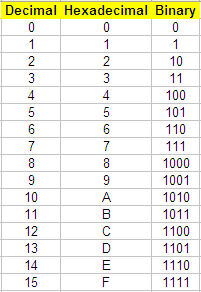
The following table shows the meaning of all the symbols in the hex (for short) numbering system.

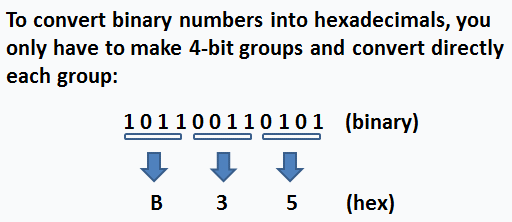
To convert a value from binary to hexadecimal, you merely translate each 4-bit binary group to its hexadecimal equivalent. For example, the binary number 0011 1111 0111 1010 translates into the hex 3F7A equivalent. 

Solution 1. 

In Matlab, we can go from binary to decimal, and then, from decimal to hexadecimal. We can embed one instruction into the other, like this: 

hex_str = dec2hex(bin2dec(bin_str))

 
It’s important to remember that both binary numbers and hexadecimal ones are treated as strings in Matlab. 

So, we can use this concept, like this:

bin_str = '10001011110101'
hex_str = dec2hex(bin2dec(bin_str))

 
Matlab’s answer is: 

hex_str = 22F5

Solution 2.

We can develop a function to translate the table shown before. Our proposed method uses a switch-case structure.
 

% Binary to Hexadecimal conversion
function h = b2h(b)
switch b
    case {'0', '00', '000', '0000'}
        h = '0';
    case {'1', '01', '001', '0001'}
        h = '1';
    case {'10', '010', '0010'}
        h = '2';
    case {'11', '011', '0011'}
        h = '3';
    case {'100', '0100'}
        h = '4';
    case {'101', '0101'}
        h = '5';
    case {'110', '0110'}
        h = '6';
    case {'111', '0111'}
        h = '7';
    case '1000'
        h = '8';
    case '1001'
        h = '9';
    case '1010'
        h = 'A';
    case '1011'
        h = 'B';
    case '1100'
        h = 'C';
    case '1101'
        h = 'D';
    case '1110'
        h = 'E';
    case '1111'
        h = 'F';
end

 
Now, we have to call the function for every 4-bit group of binary numbers. One possible solution to separate the binary number into 4-bit groups is shown here:

 
bin_str = input('Enter binary number: ', 's');
i = length(bin_str);
n = ceil(i/4); 

for g = n : -1 : 1
    if i > 4
        hex_str(g) = b2h(bin_str(i-3 : i));
        i = i - 4;
    else
        hex_str(g) = b2h(bin_str(1 : i));
    end
end
hex_str 

Let’s try it. 

Enter binary number: 101010
hex_str = 2A 

Enter binary number: 110001011110101
hex_str = 62F5