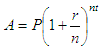Calculate Simple Interest and Compound Interest – easy exercises with MatlabWe’ll see how to calculate the simple interest and the compound one in this article. We have to start with some definitions, though.
|
Let's create our code! - Example
Find the amount of an
investment if $10,000 is invested at 5%
compounded monthly for three years.
Fortunately, we can
create a function in Matlab for the
compound interest formula, like this:
function A =
comp_int(P, r, n, t)
A = P*(1
+ r/n)^(n*t);
and we can call it from
another m-file, script, or from the
command window, in this way:
P =
10000;
r =
0.05;
n = 12;
t = 3;
format bank
A
=
comp_int(P, r, n, t)
The answer is:
A = 11614.72
3.- Continuously Compounded Interest
When the interest is
compounded more frequently, we get to a
situation of continuously
compounded interest. This formula works it out:
A = Pert
where
A = amount, or ending balance
P = principal
e = 2.718281...
t = number of years
r = annual interest rate
Example
Find the amount of an
investment if $10000 is invested at 5%
compounded continuously for three years.
Fortunately again, we can
create another function to
calculate the formula above, like this:
function A =
comp_int_2(P, r, t)
A = P *
exp(r*t);
and we can call it from
another script or from the command
window, in this way:
P = 10000
r = 0.05
t = 3
A =
comp_int_2(P, r, t)
The answer is:
A = 11618.34
From 'Calculate Simple Interest ' to home
From 'Calculate Simple Interest ' to Finance Formulas
| Top Online calculator Future value Salvage value Initial investments Effective interest rate Calculate loan payment |