De Morgan Laws - Boolean logic

In Boolean Algebra, there are some very important laws which are called the De Morgan's laws (the spelling can change from author to author).

These laws teach us how to interchange NOT with AND or OR logical operators.

In formal logic, De Morgan's laws are rules relating the logical operators 'and' and 'or' in terms of each other via negation:

not(p or q) =
(not p) and (not q)

not(p and q) =
(not p) or (not q)

Using logic gates (commonly used in Digital Electronics), they can be expressed in two forms:

the OR form: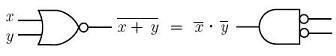
De Morgan's laws

the AND form: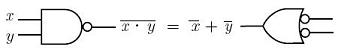
DeMorgan's law

In Matlab, these laws can be confirmed very easily.
Let's create a script file like this:

% Let x and y be column vectors
x = [0 0 1 1]'
y = [0 1 0 1]'

% We can confirm the OR form of the law with these two lines
x_or_y = x|y
DeMorg1 = not(not(x)& not(y))

% We can verify the AND form of the law with these two lines
x_and_y = x&y
DeMorg2 = not(not(x) | not(y))

When we run it, we get this output:

x = 0 0 1 1	y = 0 1 0 1
x_or_y = 0 1 1 1	DeMorg1 = 0 1 1 1
x_and_y = 0 0 0 1	DeMorg2 = 0 0 0 1

Which confirms the De Morgan's laws.

From 'De Morgan laws' to home
From 'De Morgan laws' to 'Boolean Algebra' Menu

Top

Boolean Axioms

Logic Operators

footer for de morgans laws page