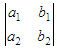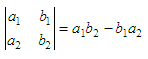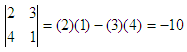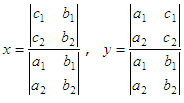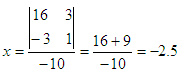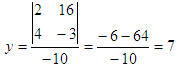Determinants in MatlabThe determinant (in linear algebra) is a value associated with a square matrix, that is a matrix with as many rows as columns. It can be calculated from the elements of the matrix by a specific arithmetic expression. The determinant provides important information in many types of problems, for example, when the matrix represent the coefficients of a system of linear equations...
which consists
of the four numbers a1,
b1,
a2,
b2
arranged in two rows and two columns is called a determinant of second order
or of order two.
The four numbers are called its elements. By definition,
Here, the elements 2 and 3 are in the first
row, and the
elements 4 and 1 are in the second row. Elements 2 and 4 are in column
one, and
elements 3 and 1 are column two. The
method of solution of
linear equations by determinants is called the Cramer’s
Rule. A system of two linear equations in two unknowns may
be solved using a
second order det.
Given the system of equations a1x + b1y = c1
a2x + b2y = c2 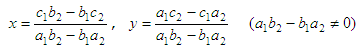
Solve the system of equations:
In
Matlab, a determinant can be calculated with the built-in function
'det()'.
if A =
[2 3; 4 1], then det(A) = -10;
From 'determinants' to 'Linear Algebra' |