

Dot Product (also known as Inner or Scalar Product)The dot product is a scalar number and so it is also known as the scalar or inner product. In a real vector space, the scalar product between two vectors  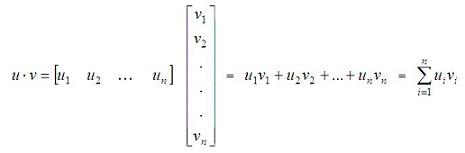 Besides, there is another way to define the inner product, if you know the angle between the two vectors: 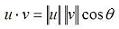 We can conclude that if the inner product of two vectors is zero, the vectors are orthogonal. In Matlab, the appropriate built-in function to determine the inner product is 'dot(u,v)'. For example, let's say that we have vectors u and v, where u = [1 0] and v = [2 2]. We can plot them easily with the 'compass' function in Matlab, like this: x = [1 2] y = [0 2] compass(x,y) x represents the horizontal coordinates for each vector, and y represents their vertical coordinates. The instruction 'compass(x,y)' draws a graph that displays the vectors with components (x, y) as arrows going out from the origin, and in this case it produces: 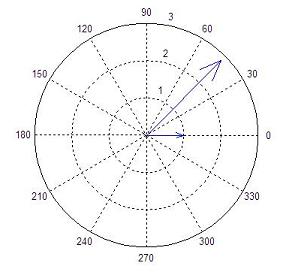 We can see that the angle between the two vectors is 45 degrees; then, we can calculate the scalar product in three different ways (in Matlab code): a = u * v' b = norm(u, 2) * norm(v, 2) * cos(pi/4) c = dot(u, v) Code that produces these results: a = 2 b = 2.0000 c = 2 Note that the angle has to be expressed in radians, and that the instruction 'norm(vector, 2)' calculates the Euclidian norm of a vector (there are more types of norms for vectors, but we are not going to discuss them here). From 'Dot Product' to home From 'Dot Product' to 'Matlab Examples'
|
