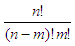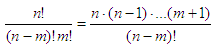Factorials – several ideas to code them

Four methods to code and calculate factorials

The factorial operation is found in many areas of math, mainly in probability and statistics, combinatorics, algebra and data analysis. Its most basic appearance is due to the fact that there are n! ways to arrange n distinct elements into a sequence (permutations of any set of objects). 

There are a number of solutions when we have to code factorials and we can experiment with any number-crunching software.
 

1. Function ‘factorial’

In Matlab, we can use built-in function ‘factorial’, like this:

n = 9
% use function factorial
factorial(n) 

The answer is 362880.

2. Function ‘prod’

We can also use built-in function ‘prod’. For vectors, prod(n) is the product of the elements of n. For matrices, prod(X) is a row vector with the product of each column.

n = 9
% use function prod, which multiplicates
% every element in a vector
prod([1 : n]) 

The answer is, again, 362880.

3. Iterations

We can use iterations to get the multiplication of numbers, just following the definition of what a factorial is 

n = 9
% use iterations
f = 1;
for i = 1:n
    f = f*i;
end
f

4. Recursion

We could even use a recursive method to calculate a factorial. That idea and method is explained in detail in the article recursion.

Custom-made formula

Now, if we want to calculate a custom-made formula including factorial operations, we can create and optimize a function for that specific purpose. Let’s say that we need to calculate

 

without using the Matlab factorial function. As a condition, we may assume that the user will know that n > m, and that n and m are positive integers.

We can optimize the code, since we know in advance that

Thus, our customized function could be: 

function y = special_fact(n, m)
% using 'prod' and appropriate vectors
y = prod([m+1 : n]) / prod([1 : n-m]); 

or another possibility
 

function y = special_fact1(n, m)
% using loops to calculate the numerator
f1 = 1;
for i = m+1 : n
    f1 = f1 * i;
end
% using loops to calculate the denominator
f2 = 1;
for i = 1 : n-m
    f2 = f2 * i;
end
% assembling the appropriate terms
y = f1/f2;

 

Let’s test our functions:

n = 19;
m = 13;
factorial(n)/(factorial(n-m)*factorial(m))
special_fact(n,m)
special_fact1(n,m)

And all the answers are 27132.

Double Factorials

n = input('Give me a number: ');
df = 1;
for i = n : -2 : 1
    df = df * i;
end
str = ['Double Factorial of ' num2str(n) ' is ' num2str(df)];
disp(str)