

Fibonacci Numbers in Matlab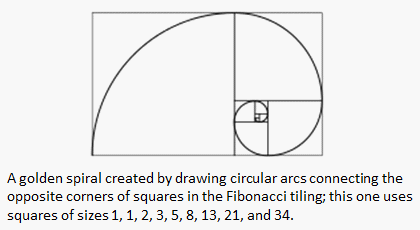 The first two Fibonacci numbers are 0 and 1, and each remaining number is the sum of the previous two. Some sources neglect the initial 0, and instead beginning the sequence with the first two ones. The Fibonnacci numbers are also known as the Fibonacci series. Two consecutive numbers in this series are in a 'Golden Ratio'. In mathematics and arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity equals the ratio of the larger quantity to the smaller one. The golden ratio is an irrational constant, approximately 1.618033988. We're designing below a simple function to see how it appears... The command 'num2string' changes a number into a string, so that it can be included in another string. The command 'num2str(golden_ratio, 10)' shows the number 'golden_ratio' with 9 digits after the decimal point. The simple code is here: %Clear
screen and memory %
Initialize the first two values %
Create the first 30 Fibonacci numbers
You can see that, in
fact, the quotient
of two consecutive numbers reaches the 'golden ratio' after just a few
numbers in the series. From 'Fibonacci Numbers' to home From 'Fibonacci Numbers' to 'Matlab programming' Menu
|

