

Interpolation - easy in MatlabThis page shows the most usual and general interpolation concept. This code calculates the y-coordinates of points on a line given their x-coordinates. It is necessary to know coordinates of two points on the same line. A point is interpolated using the following formula: 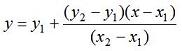 We can develop then the following Matlab function. Input parameters are the two known coordinates and the desired x-value to interpolate. Note that with this formula we can also extrapolate a coordinate on the same line. function y = interpolate(x1, y1, x2, y2, x) % Calculate corresponding y-coordinate y = y1 + (y2-y1)/(x2-x1) * (x-x1); Let's assume that our known coordinates are (60, 15.56) and (90, 32.22), and our x-values to be interpolated are 73 and 85.6. Now, we can use the above function, for example calling it like this: y = interpolate(60, 15.56, 90, 32.22, 73) y = interpolate(60, 15.56, 90, 32.22, 85.6) Matlab response is: y = 22.7793 y = 29.7765 Fortunately, Matlab has also several built-in function to interpolate values with different methods ('interp1', 'interp2', 'interp3', and 'interpn'). 'interp1' is called one dimensional interpolation because vector y depends on a single variable vector x. The calling syntax is ynew = interp1(x, y, xnew, method) The parameter 'method' can be 'nearest', 'linear', 'cubic' or 'spline'. The default method is 'linear' (type help interp1 on the Matlab command window to see more details). We can use this function (instead of our own developed function above), like this: x = [60 90]; y = [15.56 32.22]; xnew = 73; ynew = interp1(x, y, xnew) xnew = 85.6; ynew = interp1(x, y, xnew) And Matlab response is: ynew = 22.7793 ynew = 29.7765 Linear Regression Curvilinear Interp. Polynomial Fit From 'Interpolation' to home From 'Interpolation' to 'Matlab Cookbook' Top |

