Lagrange Interpolation 

(curvilinear interpolation)

The computations in this small article show the Lagrange interpolation. The code computes y-coordinates of points on a curve given their x-coordinates.

You must enter coordinates of known points on the curve, no two having the same abscissa.

This is the simple function: 

function y0 = lagrange_interp(x, y, x0)
% x is the vector of abscissas.
% y is the matching vector of ordinates.
% x0 represents the target to be interpolated
% y0 represents the solution from the Lagrange interpolation
y0 = 0;
n = length(x);
for j = 1 : n
    t = 1;
    for i = 1 : n
        if i~=j
            t = t * (x0-x(i))/(x(j)-x(i));
        end
    end
    y0 = y0 + t*y(j);
end 

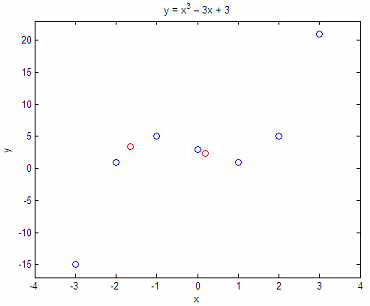
Example 1 - Interpolate a cubic function 

Consider the curve y = x³ - 3x + 3. We now that points 

x = [-3 -2 -1 0 1 2 3];
y = [-15 1 5 3 1 5 21]; 

are on the curve. What are the values of y when x = -1.65 and 0.2? 

x1 = -1.65;
y1 = lagrange_interp(x,y,x1) 

x2 = .2;
y2 = lagrange_interp(x,y,x2) 

The results are:
y1 = 3.4579
y2 = 2.4080 

Let’s plot our approach:

plot(x, y, 'bo', x1, y1, 'ro', x2, y2, 'ro')
axis([-4 4 -17 23])
title(‘y = x^3 – 3x + 3’)
xlabel(‘x’)
ylabel(‘y’)

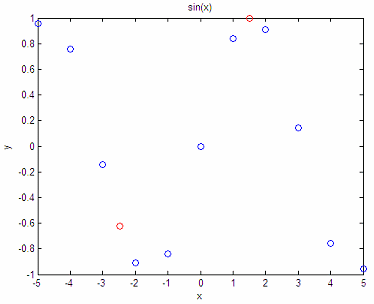
Example 2 -  Interpolate a sine function 

Given the following points from a sine curve, what are the y-values for x = -2,47 and x = 1.5? 

x = [-5 -4 -3 -2 -1 0 1 2 3 4 5];
y = [.958 .757 -.141 -.909 -.841 0 .841 .909 .141 -.757 -.959]; 

x3 = -2.47;
y3 = lagrange_interp(x,y,x3) 

x4 = 1.5;
y4 = lagrange_interp(x,y,x4)
 

The results are:

y3 = -0.6218
y4 =  0.9972

 
And our plot is:

plot (x, y, 'bo', x3, y3, 'ro', x4, y4, 'ro')
title('sin(x)')
xlabel('x')
ylabel('y')