

Linear Algebra and its Applications - Circuit AnalysisOne important linear algebra application is the resolution of electrical circuits. We can describe this type of circuits with linear equations, and then we can solve the linear system using Matlab. For example, let's examine the following electrical circuit (resistors are in ohms, currents in amperes, and voltages are in volts): 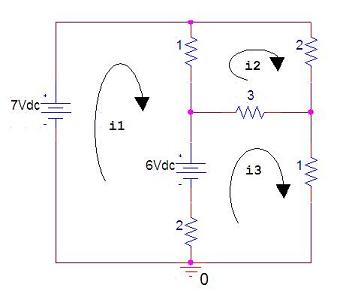 We can describe the circuit with the following system of linear equations: 7 - 1(i1 - i2) - 6 - 2(i1 - i3) = 0 -1(i2 - i1) - 2(i2) - 3(i2 - i3) = 0 6 - 3(i3 - i2) - 1(i3) - 2(i3 - i1) = 0 Simplifying and rearranging the equations, we obtain: -3i1 + i2 + 2i3 = -1 i1 - 6i2 + 3i3 = 0 2i1 + 3i2 - 6i3 = -6 This system can be described with matrices in the form Ax = b, where A is the matrix of the coefficients of the currents, x is the vector of unknown currents, and b is the vector of constants on the right of the equalities. One possible Matlab code to solve this is: A = [-3 1 2 1 -6 3 2 3 -6]; b = [-1 0 -6]'; i = A\b The Matlab answer is: i = 3.0000 2.0000 3.0000 This means that i1 = 3, i2 = 2, and i3 = 3. Linear Systems - How to Solve them in MatlabSimultaneous Eq. Electrical Calculations Electronic experiments Electronic kits From 'Linear Algebra and its Applications' to home From 'Linear Algebra and its Applications' to 'Linear Algebra Menu'
|
