

Linear Programming - (as an optimization problem)
constraints in the linear inequalities or the expression for the quantity to be optimized may be numerically complicated. We will illustrate the method of linear programming by means of a simple example giving a numerical solution. Matlab has some special functions such as 'simlp' or 'linprog' to tackle down this type of problems, but these built-in functions are not always available since they belong to special toolboxes (Simulink or Optimization toolboxes). Therefore, we are going to formulate the problem as an optimization issue, and we'll use the instruction 'fminsearch', which is an always available instruction. Let's suppose that a merry farmer has 75 roods (4 roods = 1 acre) on which to plant two crops: wheat and corn. To produce these crops, it costs the farmer (for seed, water, fertilizer, etc. ) $120 per rood for the wheat, and $210 per rood for the corn. The farmer has $15,000 available for expenses, but after the harvest the farmer must store the crops while awaiting favorable or good market conditions. The farmer has storage space for 4,000 bushels. Each rood yields an average of 110 bushels of wheat or 30 bushels of corn. If the net profit per bushel of wheat (after all the expenses) is $1.30 and for corn is $2.00, how should the merry farmer plant the 75 roods to maximize profit? We begin by formulating the linear programming problem mathematically. We express the objective (profit) and the constraints. Let x denote the number of roods allotted to wheat and y the number of roods allotted to corn. Then the expression to be maximized is clearly P = (110)(1.3)x + (30)(2)y = 143x + 60y There are some constraint inequalities, specified by the limits on expenses, storage and roodage. They are: 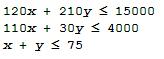 and naturally: 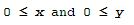 As we mentioned before, we are going to formulate this as an optimization problem using the 'fminsearch' built-in function. In Matlab, the instruction works as follows: X = FMINSEARCH(FUN,X0,OPTIONS) minimizes with the default optimization parameters replaced by values in the structure OPTIONS, created with the OPTIMSET function. FMINSEARCH uses these options: Display, TolX, TolFun, MaxFunEvals, MaxIter, FunValCheck, and OutputFcn. This is one possible approach for our objective function, which is saved as an m-file (in this case 'OF_P.m'): function OFValue = OF_P(x) % Here we embed the constraints or inequalities. % If the constraints are not met, we penalize the optimization by % giving an arbitrary high value to the objective function. if 120 * x(1) + 210 * x(2) > 15000 |... 110 * x(1) + 30 * x(2) > 4000 |... x(1) + x(2) > 75 | ... x(1) < 0 |... x(2) < 0 OFValue = 10; return end % fminsearch tries to minimize the function, so we invert its sign P = 143 * x(1) + 60 * x(2); OFValue = -P; Then, we can call it from another script, which includes the 'fminsearch' function calling the objective function file (in 'OF_P'): clear; clc; format bank % We have to start with a 'seed' for the search x = [1 10]'; % We can perform the optimization with different number of % iterations or tolerances options = optimset('MaxFunEvals', 2000, 'TolX', 1e-2); [x_opt, FunVal, EF, output] = fminsearch('OF_P', x, options) % Finally, we display the profit using the found solution P = 143 * x_opt(1) + 60 * x_opt(2) And the Matlab response is: x_opt = 21.87 53.12 FunVal = -6315.62 EF = 1.00 output = iterations: 121.00 funcCount: 243.00 algorithm: 'Nelder-Mead simplex direct search' message: [1x196 char] P = 6315.62 This means that the farmer should consider 21.87 roods for wheat, 53.12 roods for corn, and his profit would be $6,315.62. It is important to notice that this is a numerical approximation, which means that if we start with another 'seed' or use other parameters in the 'options' set, we can get to another result. The number found is a possible solution, but there's no guarantee that it is the best one, according to tolerances or to number of iterations or evaluations desired. For example, we can use the seed 'x = [10 10]' instead (without moving any other instruction), and the Matlab answer now is: x_opt = 32.31 14.88 FunVal = -5512.50 EF = 1.00 output = iterations: 75.00 funcCount: 151.00 algorithm: 'Nelder-Mead simplex direct search' message: [1x196 char] P = 5512.50 Now, the 'best' profit found is only $5,512.50. So, it is a good idea to try with several 'seeds' and different parameters in the 'options' set to compare with and select the best solution. Most of the times the solutions will be very close (at least for linear programming problems). From 'Linear Programming' to home From 'Linear Programming' to 'Linear Algebra'
|

