logo for matrixlab-examples.com
leftimage for matrixlab-examples.com

loglog - logarithmic plot


In this example we are going to demonstrate how to use the 'loglog' function included in Matlab to produce non-linear plots.

This term refers to the fact that the plot is logarithmically scaled in both axes. There are other functions such as 'semilogx' and 'semilogy' which have one axis in linear scale and the other axis in logarithmic scale.
 



1.- Create a plot using a logarithmic scale for both the x-axis and the y-axis (loglog):

clear; clc; close all 

% Define your independent variable
t = 0 : 2*pi/360 : 2*pi; 

% Define values along your x-axis
x = exp(t);
% Define values along your y-axis
y = 50 + exp(3*t); 

% Plot your function with a wider line and grid the figure
loglog(x, y, 'LineWidth', 2)
grid 

% Use a title for the figure
title('Demonstration of logarithmic plots') 

% Label your x-axis with a double line.
% Note the special characters
xlabel([{'e^{t}'}; {'0 \leq t \leq 2\pi'}]) 

% Label your y-axis
ylabel('50 + e^{3t}')



The produced figure is: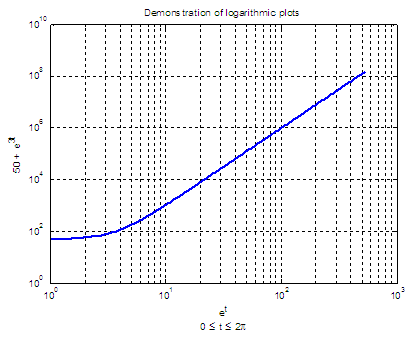

logarithmically scaled plot, produced with the Matlab function 'loglog'


2.- Create a plot with a logarithmic scale for the x-axis and a linear scale for the y-axis (semilogx):

% clear memory data and command window
clear; clc; close all

% define your linear data
x = 0 : 1000;
% define your logarithmic function
y = log(x);

% plot your log function on linear data
semilogx(x, y)

% define values of axes and grid
axis([1 1000 0 7])
grid

% add relevant info
title('Example of Semilogx')
xlabel('x')
ylabel('y = log(x)')


The resulting figure is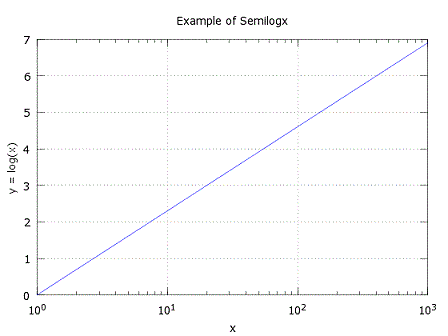

log x and linear y - semilogx example

3.- Create a plot with a logarithmic scale for the y-axis and a linear scale for the x-axis (semilogy):

clear; clc; close all

% now your data along the x-axis is linear
x = 0 : 0.5 : 10;

% your function is now exponential
y = exp(x);

% see the plot
semilogy(x, y)
plot

% add info
title('Example of Semilogy')
xlabel('x')
legend('y = e^x')

The plot is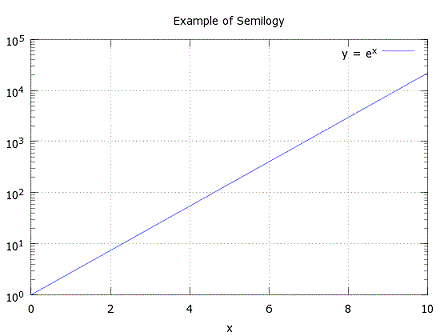


semilogarithmic plot


 From 'loglog' to home

 From 'loglog' to '2D Plot Menu'
 
Top

Table of Contents

2D summary

3D summary


footer for loglog page