Examples: Basic Matlab Codes
>> 5^3/(2^4+1) ans = 7.3529 To compute this formula: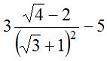 
, you can always break
down the commands and simplify the code (a final value can be achieved
in several ways).>>numerator = 3 * (sqrt(4) - 2) numerator = 0 >>denominator = (sqrt(3) + 1)^2 denominator = 7.4641 >>total = numerator/denominator – 5 total = -5 The following expression: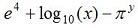 
, can be achieved as
follows (assuming that x
and y have
values already):>> exp(4) + log10(x) - pi^y The basic MATLAB trigonometric functions are 'sin', 'cos', 'tan', 'cot', 'sec', and 'csc'. The inverses, are calculated with 'asin', 'atan', etc. The inverse function 'atan2' takes two arguments, y and x, and gives the four-quadrant inverse tangent. Angles are in radians, by default. The following expression: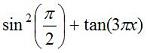 
, can be coded as
follows (assuming that x
has a value already):>>(sin(pi/2))^2 + tan(3*pi*x). MATLAB recognizes the letters i and j as the imaginary number. A complex number 4 + 5i may be input as 4+5i or 4+5*i in MATLAB. The first case is always interpreted as a complex number, whereas the latter case is taken as complex only if i has not been assigned any local value. Can you verify in MATLAB this equation (Euler's Formula)? You can do it as an exercise! 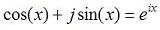 From 'Matlab Codes' to home From 'Matlab Codes' to 'Matlab Examples'
|
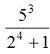, you can write the
following instruction in the Matlab command window (or within an 
