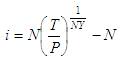Nominal Interest Rate on Investments - Calculation

 
The Nominal Interest Rate is based on the following formula:

 
where:
i = nominal interest rate
P = initial investment
T = future value
N = number of compounding periods per year
Y = number of years
 

The nominal interest rate is expressed as a yearly rate even though the interest rate used when compounding interest is i/N. The nominal interest rate will be less than the effective interest rate when interest is compounded more than once a year. This is because the nominal rate stated doesn’t take into account interest compounded on interest earned in earlier periods of each year.
 

This is our simple Matlab code to calculate the formula above: 

function it = nominal_interest_rate(p, t, n, y)
it = n*((t/p)^(1/(n*y))-1)*100;
 

We create another script to test and drive the above m-file: 

clc; clear; format bank 

p = input('Enter principal: ');
t = input('Enter total value: ');
y = input('Enter number of years: ');
n = input('Enter number of compounding periods per year: '); 

int_rate = nominal_interest_rate(p, t, n, y)

Example 1:

Jean invests $945 in a savings bank. Four and a half years later her investment amounts to $1309.79. If interest is compounded monthly, what is the nominal interest rate offered by the bank?

Enter principal: 945
Enter total value: 1309.79
Enter number of years: 4.5
Enter number of compounding periods per year: 12 

The result is:

int_rate = 7.28
 

Example 2: 

David invests $3000. Ten years later he has earned $1576 in interest. If interest is compounded each month, what is the nominal interest rate on the account?

Enter principal: 3000
Enter total value: 4576
Enter number of years: 10
Enter number of compounding periods per year: 12 

The result is:

int_rate = 4.23