Periodic function – some codes without special toolboxes in Matlab

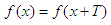for all values of x. The least positive constant T with this property is called the period. A function with period T will repeat on intervals of length T. These intervals are referred to as periods.

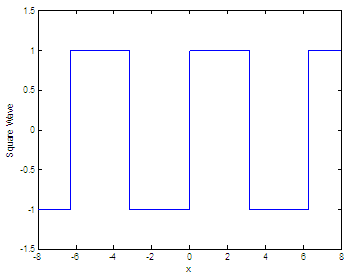
In this article, we’re going to develop and plot two common periodic functions (square and sawtooth waves) without using any special Matlab toolbox, so that we could use or translate these algorithms into any other programming language.
 

Square wave

A square wave is similar to a sinusoidal waveform but with very abrupt changes, very typically encountered in electronics and signal processing. An ideal square wave is a periodic function that changes or alternates regularly and suddenly between only two levels.

Square waves are encountered in switching circuits (digital electronics) and are generated by binary (only two-value) logic devices. They are often used as timing references or ‘clock signals’, because their transitions are appropriate for triggering logic circuits at exactly determined intervals.

Our first approach for this wave will be a typical scalar function. We can use for-loops to inspect every value (x_i) of the input vector. If we detect that x_i is in the first half of the period, we’ll set a ‘high’ value; if x_i is in the last half of the period, we’ll set a ‘low’ value for the function.

Our function generates a square wave with period 2π for the elements of time vector x.  Function sq_w(x) is like sin(x), only it creates a square wave with peaks of +1 to -1 instead of a sine wave. 

function y = sq_w(x)
% We'll inspect every value of the vector
for i = 1 : length(x)
    % Total length of high and low values are pi
    t = ceil(x(i)/pi);
    if mod(t, 2)==0
        % if x(i) is in the last half, we set a -1
        y(i) = -1;
    else
        % if x(i) is in the first half, we set a +1
        y(i) = 1;
    end
end

We can call our function like this, from another script (maybe called ‘test_sq_w.m’) or from the command window:
 

clear, clc, close all 

x = -8 : .01 : 8;
y = sq_w(x);
plot(x,y)
axis([-8 8 -1.5 1.5])
xlabel('x')
ylabel('Square Wave')
 

The result is:

The second approach is smarter. We don’t use for-loops and so the function is called to be vectorized. We use only three lines of code:

function y = sq_w(x)
% we set a default value of 1
y = ones(1, length(x)); 

% we find elements in the second half of the period by
% dividing every cycle in two. The first half is odd,
% the second half is even
t = mod(ceil(x/pi), 2) == 0; 

% we set a -1 only for elements in the second
% half of every period
y(find(t)) = -1;

We call it with our function above ‘test_sq_w.m’ and the result is exactly the same as the shown before.

Our third approach is much simpler. We use the standard ‘sin(x)’ function but change all the function’s positive values to 1 and all the negative values to -1.

 
function y = sq_w(x)
y = sin(x); 

% we find positive elements and represent them as 1
y(find(y >= 0)) = 1; 

% we find negative elements and represent them as -1
y(find(y < 0)) = -1;

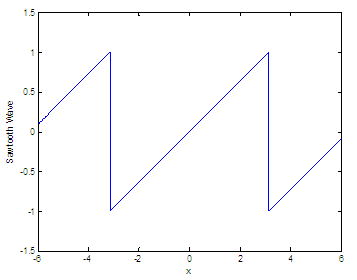
If we test the function, the result is the same as before.

Sawtooth wave

The sawtooth wave is another periodic function and a kind of non-sinusoidal waveform. It is named a sawtooth due to its resemblance to the teeth on the edge of a saw. The common use is that a sawtooth wave goes upward and then sharply drops.
 

An application of the sawtooth wave is the form of the vertical and horizontal signals used to generate a trace on CRT-based televisions or monitor screens. Oscilloscopes also use a sawtooth wave for their horizontal deflections. 

Our sawtooth function has the same phase and period as a sine function.

Function sawtooth_w(x) generates a sawtooth wave with period 2π for the elements of time vector x.  sawtooth_w(x) is like sin(x), only it creates a wave with peaks of +1 to -1 instead of a sine wave.
 

Basically, we want y = x (a very informal way to describe it) but reset or repeated every period. We have to take into account that the output value repeats every 2π cycle.

 
function y = sawtooth_w(x)
% We find the period number of every element
% in the input vector
tn = ceil((x+pi)/(2*pi)); 

% and we subtract that corresponding period from
% the base value. We want final values from -1 to 1
y = ((x - tn*2*pi) + 2*pi)/pi; 

We run our function, like this (with a script named ‘test_saw_w.m’):

clear, clc, close all 

x = -6 : .01 : 6;
y = sawtooth_w(x);
plot(x, y)
axis([-6 6 -1.5 1.5])
xlabel('x')
ylabel('Sawtooth Wave')
 

and the Matlab resulting plot is: