Polar Plots (with a little help from Matlab)

Matlab provides functions that plot data in the polar coordinates using magnitudes and angles. In this article we’ll discuss and show the Matlab built-in commands 'compass', 'polar' and 'rose'.

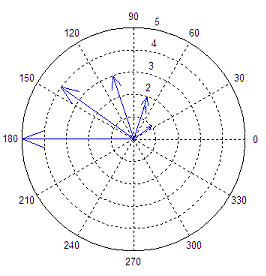
The Compass Function 

The compass function takes its inputs in Cartesian format, but outputs polar plots. In the compass function each arrow’s length corresponds to the magnitude of a data element and its pointing direction indicates the angle of the complex data. This function creates arrows that go out from the origin of the axes in a polar coordinate system. To illustrate this function, we’ll create a set of arrows that increase in size from arrow to arrow in a counter-clockwise manner. 

t = 1 : 5;
r = t .* exp(i * t * 36 * (pi/180));
compass(r)
 

This code produces:

The Polar Function

The polar function creates polar plots from angle and magnitude data.

It takes the forms polar(theta,rho), where theta corresponds to the angle (in radians) and rho corresponds to the magnitude. The variables theta and rho must be identically sized vectors. 

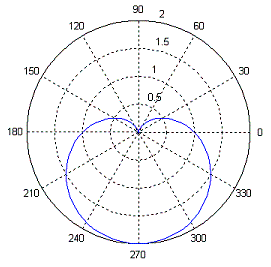
As an example, we create a cardioid with the following code: 

t = 0 : 2*pi/100 : 2*pi;
r = 1 - sin(t);
polar(t, r)

Here’s the result:

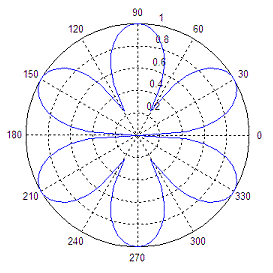
Here’s another polar chart: 

t = 0 : 2*pi/100 : 2*pi;
r = sqrt(abs(sin(3*t)));
polar(t,r)

The Rose Function

With rose you can create angle histograms that are drawn in polar coordinates. By using rose(angle_data), the function will determine how many of the angles (in radians) fall within a given angular bin. By default there are 20 evenly spaced bins between 0 and 2pi. The number of bins can be changed by using rose(angle_vector, nr_of_bins), where the variable nr_of_bins is a scalar specifying the number of bins that should be spaced between 0 and 2pi. You can also specify the centers of the bins by passing a vector, bin_centers, to the rose function, like this: rose(angle_vector, bin_centers). 

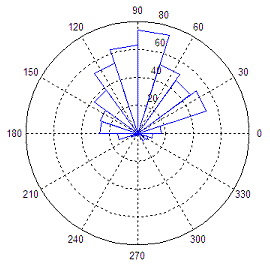
The following code produces a rose plot of data which is normally distributed in angle about 90º.
 

angle_vector = angle(exp(i*randn(1, 500))) + pi/2;
rose(angle_vector)
 

This is the result of the angle histogram created with rose: