

Random Numbers and Simulations
AveragesThe mean is given by adding up all the data and dividing by the number of objects in the set. This is written as: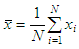 There’s a Matlab command
which does exactly this: ‘mean(x)’. There’s another related
command, which is ‘median(x)’
and it’s
the value in the ‘middle’ of a vector when the data has been sorted. If there’s
an odd number of pieces of data this is well defined, however if the
number is
even then the mean of the data at each end of the central interval is
given,
for example the median of [1 2 3 4] is (2+3)/2 = 2.5 whereas the median
of [1 3
5] is 3. Note that the median can equal the mean but it is not
necessarily so. This short code x = [4 0 5 3 2 1 3 5 9 3 7 5 6 8 2 0]; results in mn = 3.9375 |
 |
 |
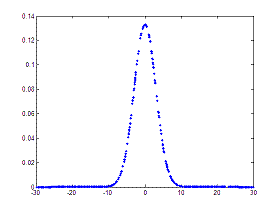
The first curve is narrower than the second and this is quantified using the variance, which is given by
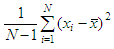
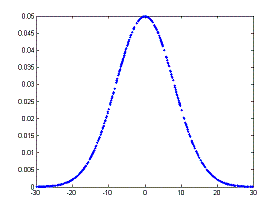
We can interpret this value as the ‘mean’ of the sum of the squares of the distance from the mean. There’s the Matlab command ‘var(x)’ to calculate this number. Another related measure is the standard deviation, which is the square root of the variance, ‘std(x)’. This also is a measure of the width of the distribution and has the advantage that it has the same units as the data.
There are other measures, some of which are called ‘higher-order moments’ (mean is first and variance is second): the skewness is the third, and the kurtosis is the fourth.
Random Numbers and Distributions
In order to generate
random numbers we can use various
commands available
in Matlab. We won’t worry about how this is done or the
technical aspects of the seeding. We’re going to start with the simple
command
‘rand’ which
returns a random number between zero and one.
If we rolled a die a
large number of times, and we used the
above formulas to calculate the mean and variance, we’d expect to
obtain a mean
= 3.5 and a variance = 2.916. Let’s try it with Matlab.
This is a simple dice program:
function n =
roll_d()
n =
ceil(rand*6 + eps);
We can use it like this:
%
Roll the die and keep the values in d
for i = 1 :
1000
d(i)
= roll_d;
end
%
Find how many appearences of each possible value
for i = 1 :
6
v(i)
= length(find(d==i));
end
%
Display results
disp(['Mean
= '
num2str(mean(d))])
disp(['Variance
= '
num2str(var(d))])
bar(v)
The results are:
Mean = 3.508
Variance = 2.7827
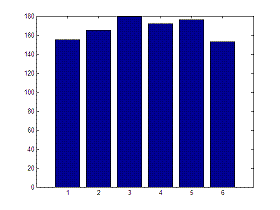
Obviously, every time that we run the program we’ll get different results, since we are dealing with random numbers, but the results are similar to what we expected.
We can use this process
for other ‘chance games’,
for
example tossing a coin:
function r =
toss()
p = ['heads'; 'tails'];
i =
ceil(rand*2 + eps);
r =
p(i,:);
This can then be called just using 'toss'
which generates
either 'heads' or 'tails'.
Normal Distribution
A normal distribution has
two parameters associated with it:
the mean and the variance. The command ‘randn’ generates
random
numbers which have a mean
of zero and a variance
of unity.
By typing
x = randn(1, 1000);
hist(x,12)
we set up an array and produce the plot
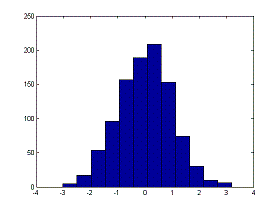
mn = mean(x)
v =
var(x)
produce, in our case
mn = 0.0016
v =
0.9908
There are many problems which require simulation, largely due to that it's not viable to actually run the real or physical tests. These cases cover things from experiments on aircrafts or cars (which are too dangerous or expensive) to population studies and economic strategies.
From 'Random Numbers' to homeFrom 'Random Numbers' to 'Probability and Statistics'
| Top Gaussian Distribution More on Random Nrs. |
