[?] Subscribe To This Site

Simpson's Rule

This code approximates the definite integral of a function. The integral is calculated using Simpson's rule.

You must supply the limits of integration, the increment between points within the limits, and the function of the curve to be integrated.

For example, if we want to integrate the function f(x) = y = x³, we can define it, in Matlab, like this:

function y = fun_for_integration(x)
y = x^3;

And then, we can create the actual integration function, like this:

function y = simpson2(lower_lim, upper_lim, incr, fun)

% Check that the provided increment has sense for our purpose
if (upper_lim - lower_lim)/incr ~= floor((upper_lim - lower_lim)/incr)
    disp('Warning: increment must divide interval into equal subintervals')
    disp('Please change the increment')
    y = 'error';
    return
end

% Evaluate the function in the lower and upper limits
y1 = feval(fun, lower_lim);
y2 = feval(fun, upper_lim);

% Initialize the intervals
c = 0;
d = 0;

% Loop for each subinterval
for i = 1 : (upper_lim - lower_lim)/incr - 0.5;

    % Calculate the function at each subinterval
    y = feval(fun, lower_lim + i*incr);

    % Interval even or odd?
    if i/2 == floor(i/2)

        % Sum all even-interval function values
        d = d + y;
        continue
    else
        % Sum all odd-interval function values
        c = c + y;
        continue
    end
end

% Calculate integral
y = incr/3 * (y1 + 4*c + 2*d + y2);

Now, we can call our integration function from another Matlab script or from the command window, for example

z1 = simpson2(0, 2, .01, 'fun_for_integration')
z2 = simpson2(0, 2, .2, 'fun_for_integration')

and we get the Matlab results, which in this case are the same

z1 =
4.0000
z2 =
4

Note that this is a numerical integration, and so we have to be very aware of the inaccuracies of the Simpson's Rule method. The first two parameters given to the function are the lower and upper limits, respectively. The third parameter is related to the size of each interval. The fourth parameter is the name of the function to be integrated (the instruction 'feval' is in charge of evaluating that function in the main body of the integration code).

Now, the best part is that Matlab has its own function to do the integration using the Simpson's rule ('quad'), so we can save all of our programming efforts for other things...

However, the built-in 'quad' function, works a little different. It integrates a specified function over specified limits, based on adaptive Simpson's rule. This adaptive rule attempts to improve accuracy by adaptively selecting the size of the subintervals (instead of keeping it constant) within the limits of integration while evaluating the sums that make up the integral.

You can call this 'quad' function, like this

z = quad('fun_for_integration', 0,2)

and Matlab response is

z =
4

Now, let's integrate another function. Let's work on this: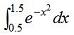

First, we define the function to be integrated in Matlab, in this way

function y = fun_for_integration2(x)
y = exp(-x.^2);

Then, we can call the 'quad' function from another script or try it from the Matlab command window, like this

z = quad('fun_for_integration2', 0.5, 1.5)

The Matlab result is

z =
0.3949

Top
<Trapezoidal Rule>

From 'Simpsons Rule' to home
From 'Simpsons Rule' to 'Matlab Cookbook'

footer for simpsons rule page