

Square
root algorithm (example on while-loops)
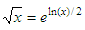 The
most common iterative method of square root calculation is known as the
‘Heron's
method’ or ‘Babylonian
method’. First
step, estimate a number. Think of this number as your
first approach to a root (the
closer to the actual square root of x,
the fewer iterations will be needed to achieve the desired precision). Second
step, divide your number by this (known inexact) square
root. Third
step, take the average of the result of the second step
and ‘the root’. Fourth
step, use the result of the third step to repeat steps 2
and 3 until you have a
number that is accurate enough for you. The
technique is a variation of the Newton-Raphson
iterative solution method and
it involves a simple algorithm, which results in a number closer to the
actual
square root each time it is repeated. A code
that accomplishes the algorithm is: function ta =
sr(x) %
Repeat until you obtain a good enough root We can
use or try our function like this, from the command window for example: format long ta
= 3.17857142857143
y1
= 3.16227766016838 Another
example, y3
=
sr(255) ta
= 34.34411196911197 Our
algorithm needed six iterations to obtain the final result (in y3,
below). Note
that only four iterations were needed to have an accuracy within one
decimal.
y4 is the result from the function ‘sqrt’, to compare with. y3
= 15.96871942267163 From 'Square Root algorithm' to home From 'Square Root algorithm to 'Flow Control'
|
