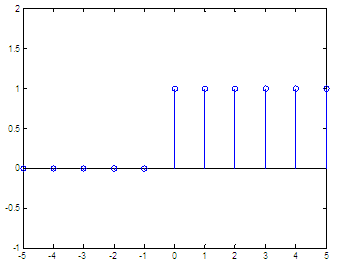
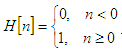Heaviside Unit Step FunctionThe unit step function (also known as the Heaviside function) is a discontinuous function whose value is zero for negative arguments and one for positive arguments. The Heaviside function is the integral of the Dirac delta function.
Our current intention is not to deal with all the formal details. In this brief article we're going to deal with it in an informal way, in order to just operate with it and create some plots in Matlab.
The
function depends on real input parameters. function y =
step_fun(n) %
We change our output to 1 if the argument is greater
%
We iterate from -5 to 5 using only integers
Now,
let’s say that we have a vector (not a scalar) as an input. We want to
calculate the Heaviside function for all of the values
included in the vector.
We can create another function to considerate this approach: function y =
heaviside(n) %
Our default output value is 0
n = -5 :
5;
If we
want to calculate y = 4H(n)
+ 3H(n-2), in
a range of integers that go from -10 to 10, we can do
simply this: n = -10 : 10; and the
result is: 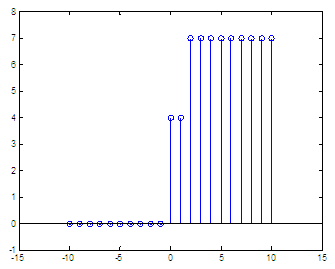 We can see that every integer in the domain of the function counts to add to the final result, and that happens when the argument is zero for each term. The first term, 4H(n), adds a height of 4 (coefficient) at n = 0; the second term, 3H(n-2), adds a magnitude of 3 at n = 2. From 'Step Function' to home From 'Step Function' to 2D-plots Menu
|