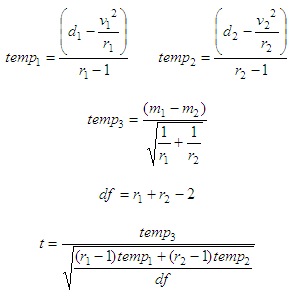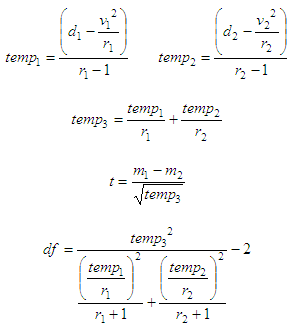T-statistic 

Student’s t-distribution Test

 This program performs the t-statistic and degrees of freedom for Student’s distribution, in Matlab code. The calculations can be based on any one of these three hypotheses.

The first hypothesis assumes that one population mean is equal to a given value. You must enter the elements of the sample and the value of the mean.
 

We are going to implement the following formulas: 

First case: one sample given, one mean assumed

where:
t = t-statistic result
df = degrees of freedom
v = sum of elements
d = sum of squared elements
r = number of elements in sample
m = mean of current sample
gm = assummed mean
 

This is how we can implement the formulas in Matlab: 

function [t, df] = t_test1(gv, gm)
% Inputs: gv = given vector
%         gm = assumed mean
% Outputs: t = t-test
%          df = degrees of freedom 

% number of elements in vector
r = length(gv);
% sum of elements
v = sum(gv);
% sum of squared elements
d = sum(gv.^2);
% mean of current vector
m = mean(gv); 

% calculation of t-test and degrees of freedom
% Case 1: one vector with assumed mean
av = (d - v^2 / r) / (r - 1);
t = (m - gm) * sqrt(r/av);
df = r - 1;
 

Second case: two samples given with equal mean and std. deviation

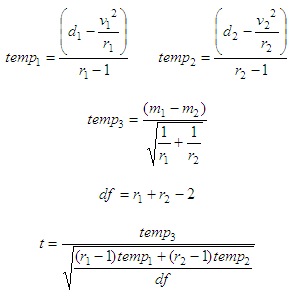
where:
t = t-statistic result
df = degrees of freedom
v_1,2 = sum of elements in samples 1 and 2
d_1,2 = sum of squared elements in samples 1 and 2
r_1,2 = number of elements in samples 1 and 2
m_1,2 = mean of samples 1 and 2
 

This is how we can implement the second case in Matlab: 

function [t, df] = t_test2(gv1, gv2)
% Inputs: gv1 = given sample 1
%         gv2 = given sample 2
% Outputs: t = t-test
%          df = degrees of freedom 

% number of elements in vector 1
r1 = length(gv1);
% sum of elements in vector 1
v1 = sum(gv1);
% sum of squared elements in vector 1
d1 = sum(gv1.^2);
% mean of vector 1
m1 = mean(gv1); 

% number of elements in vector 2
r2 = length(gv2);
% sum of elements in vector 2
v2 = sum(gv2);
% sum of squared elements in vector 2
d2 = sum(gv2.^2);
% mean of vector 2
m2 = mean(gv2); 

% calculation of t-test and degrees of freedom
% Case 2: two samples, equal mean and std. dev.
av1 = (d1 - v1^2 / r1) /(r1 - 1);
av2 = (d2 - v2^2 / r2) /(r2 - 1);
av3 = (m1 - m2) / sqrt(1/r1 + 1/r2);
df = r1 + r2 - 2;
t = av3 / sqrt(((r1-1)*av1 + (r2-1)*av2) / df); 

Third case: two samples given with equal mean but different std. deviation

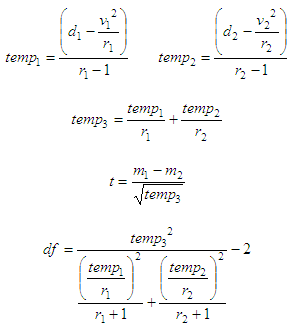
again:

t = t-test result
df = degrees of freedom
v_1,2 = sum of elements in samples 1 and 2
d_1,2 = sum of squared elements in samples 1 and 2
r_1,2 = number of elements in samples 1 and 2
m_1,2 = mean of samples 1 and 2 

This is our third case in Matlab code: 

function [t, df] = t_test3(gv1, gv2)
% Inputs: gv = given vector
%         gm = assumed mean
% Outputs: t = t-test
%          df = degrees of freedom 

r1 = length(gv1);
v1 = sum(gv1);
d1 = sum(gv1.^2);
m1 = mean(gv1); 

r2 = length(gv2);
v2 = sum(gv2);
d2 = sum(gv2.^2);
m2 = mean(gv2); 

% calculation of t-test and degrees of freedom
% Case 3: two samples, equal mean but different std. dev.
av1 = (d1 - v1^2 / r1) /(r1 - 1);
av2 = (d2 - v2^2 / r2) /(r2 - 1);
av3 = av1/r1 + av2/r2;
t = (m1 - m2) / sqrt(av3);
df = round(av3^2/((av1/r1)^2/(r1+1) + (av2/r2)^2/(r2+1)) - 2);
 

Examples: 

A sample of children’s IQs was taken, the result being 101, 99, 120, 79, 111, 98, 106, 112, 87, and 97. Calculate the t-statistic assuming the population mean is 100. 

A second sample was taken, with a result of 101, 95, 130, 150, 75, 79, 111, 100, 98, and 91. Calculate the t-statistic based on the hypothesis that the two samples have equal means and standard deviations. Calculate again supposing that the std. deviation is different between the groups. 

We can create a wrapper for the three functions above. This wrapper is useful to try and drive our code.
 

clc; clear; close all; format compact 

v1 = [101 99 120 79 111 98 106 112 87 97];
m = 100;
[t, df] = t_test1(v1, m) 

v2 = [101 95 130 150 75 79 111 100 98 91];
[t, df] = t_test2(v1, v2)
[t, df] = t_test3(v1, v2)
 

The result for the first case is: 

t = 0.2615
df = 9 

The result for the second case is: 

t = -0.2465
df = 18 

The result for the third case is: 

t = -0.2465
df = 15

From 'T statistic' to home

From 'T statistic' to 'Probability and Statistics Menu'