

Examples: Simple Vector Algebra
Something like y = mx + c. It's easy to perform algebraic operations on vectors since you apply the operations to the whole vector, not to each element alone. Now, let's create two row vectors (v and w), each with 5 linearly spaced elements (that's easy with function 'linspace'): v = linspace(3, 30, 5) w = linspace(4, 400, 5) Obtain a row vector containing the sine of each element in v: x = sin(v) Multiply these elements by their correspondig element in vector w: y = x .* w And obtain MATLAB's response: y = 0.5645 -32.9105 -143.7806 -286.4733 -395.2126 >> Did you obtain the same? Results don't appear on screen if you end the command with the ';' sign. y = x .* w; You can create an array (or matrix) by combining two or more vectors: m = [x; y] The first row of m above is x, the second row is y. m = 0.1411 -0.3195 -0.7118 -0.9517 -0.9880 0.5645 -32.9105 -143.7806 -286.4733 -395.2126 >> You can refer to each element of m by using subscripts. For example, m(1,2) = -0.3195 (first row, second column); m(2,1) = 0.5645 (second row, first column). You can manipulate single elements of a matrix, and replace them on the same matrix: m(1,2) = m(1,2)+3 m(2,4) = 0 m(2,5) = m(1,2)+m(2,1)+m(2,5) m = 0.1411 2.6805 -0.7118 -0.9517 -0.9880 0.5645 -32.9105 -143.7806 0 -391.9677 >> Or you can perform algebraic operations on the whole matrix (using element-by-element operators): z = m.^2 z = 1.0e+005 * 0.0000 0.0001 0.0000 0.0000 0.0000 0.0000 0.0108 0.2067 0 1.5364 >> MATLAB automatically presents a coefficient before the matrix, to simplify the notation. In this case 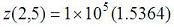 . .From 'Vector Algebra' to home From 'Vector Algebra' to 'Matlab Examples'
|
