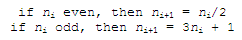Collatz Conjecture - an approach in Matlab

 
This is the sequence: take a positive integer n; if n is even, divide it by 2, and that's the next number in the sequence; if n is odd, the next number is 3n + 1 (this process has been called ‘Half or Triple Plus One’, or HPTPO). Repeat the process indefinitely... or until you reach 1. 

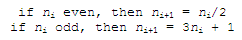
The conjecture is that no matter what number you start with, you will always eventually get to 1. So far, no one has found a case when this doesn’t happen, but the conjecture hasn’t been formally demonstrated.

A possible code in Matlab is as follows:

function [ns, seq] = collatz(n)
% Your first number in the sequence is n
seq(1) = n;
% You position an index on the next element of the sequence
i = 2; 

% Repeat the iteration until you find a 1
while seq(i-1) ~= 1
    % Use a modulus after division to find an even/odd number
    if mod(seq(i-1), 2) == 0
        % Step taken if even
        seq(i) = seq(i-1)/2;
    else
        % Step taken if odd
        seq(i) = 3*seq(i-1) + 1;
    end
    % Increment your index
    i = i+1;
end
% Find the length of the sequence
ns = length(seq);

 
Now, let’s try our Collatz-sequence function from another script or from the command window. We start with 12 and want to know the sequence and the number of elements in that sequence. 

clc; clear
[n, seq] = collatz(12) 

and we get: 

n = 10
seq = 12     6     3    10     5    16     8     4     2     1

Now, let’s say that we’d like to know what natural number up to 20 produces the longest sequence. 

We can try something like this: 

clc; clear
% We're going to start the sequences with integers up to 20
for i = 1 : 20
    % We perform the function and get the number of elements
    % in the sequence and the sequence itself
    [n(i), seq{i}] = collatz(i);
end
% We find out what's the maximum number of steps found
[max_steps, ix] = max(n)
% We display the appropriate indexed sequence
seq{ix}
    

And we get:

max_steps = 21
ix = 18
ans = 18     9    28    14     7    22    11    34    17   
      52    26    13    40    20    10     5    16     8    
       4     2     1
 

This means that if we start our sequence with 18, we get 21 elements in the sequence.

From 'Collatz Conjecture' to Matlab home

From 'Collatz Conjecture' to 'Flow Control Menu'