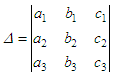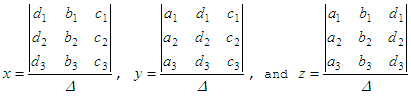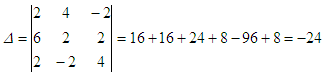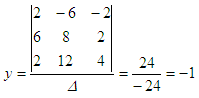Cramer's Rule

The method of solution of linear equations by determinants is called Cramer's Rule. This rule for linear equations in 3 unknowns is a method of solving by determinants the following equations for x, y, z

If we analytically solve the equations above, we obtain

If

is the determinant of coefficients of x, y, z and is

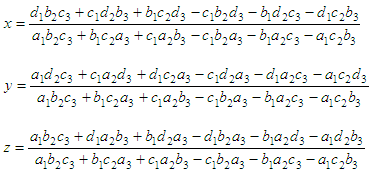
 assumed not equal to zero, then we may re-write the values as 

The solution involving determinants is easy to remember if you keep in mind these simple ideas:

• The denominators are given by the determinant in which the elements are the coefficients of x, y and z, arranged as in the original given equations.

• The numerator in the solution for any variable is the same as the determinant of the coefficients ∆ with the exception that the column of coefficients of the unknown to be determined is replaced by the column of constants on the right side of the original equations. 

Example:

Solve this system using Cramer’s Rule

2x + 4y – 2z = -6
6x + 2y + 2z = 8
2x – 2y + 4z = 12

For x, take the determinant above and replace the first column by the constants on the right of the system. Then, divide this by the determinant:

For y, replace the second column by the constants on the right of the system. Then, divide it by the determinant: 

For z, replace the third column by the constants on the right of the system. Then, divide it by the determinant: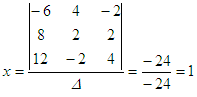

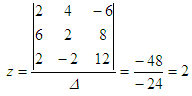
You just solved ths system!

In Matlab, it’s even easier. You can solve the system with just one instruction.

Let D be the matrix of just the coefficients of the variables:

D = [2  4 -2;
     6  2  2;
     2 -2  4]; 

Let b be the column vector of the constants on the rigth of the system :

b = [-6 8 12]'; % the apostrophe is used to transpose a vector

Find the column vector of the unknowns by 'left dividing' D by b (use the backslash), like this:

variables = D\b

variables =
    1.0000
   -1.0000
    2.0000

Top

From 'Cramers Rule' to home
From 'Cramers Rule' to 'Linear Algebra'