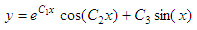Curve Fitting for experimental data
We are going to use the
simplest case for fitting a curve to
given or found data. Let’s say that we have
collected some results from an
experiment. These are the specific numbers 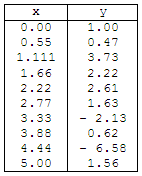
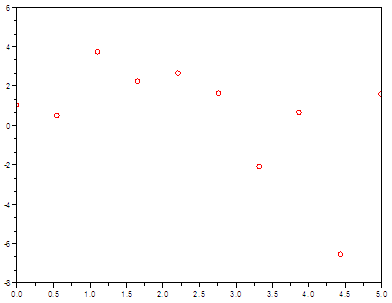
If we graph the table in
Scilab, we’re going to get this
plot
Now, let’s say that we
know in advance that those measured
or somehow collected points in our experiment are part of a nonlinear
function
of this type:
Our mission is to find
the parameters C1, C2
and C3. We know that the function
datafit is used for fitting data
to a model. For a given function G(p, z), this function finds the best
vector
of parameters p for approximating G(p, zi) = 0
for a set of
measurement vectors zi. Vector p is found by
minimizing G(p, z1)'
WG(p, z1) + G(p, z2)'
WG(p, z2) + ... + G(p, zn)'
WG(p, zn) where
datafit is an improved version of fit_dat, also available in Scilab. The first step in our
demonstration is to create a file
(called OF_datafit1.sci)
that includes our parameterized function (in this case
called data_fit_1)
and our way to measure the error (in this case the function
is called myerror). This is one way to do
it: // This function takes vector x and the
parameters // This is a way to measure the error, to
find the least one. Now, we can create a main
script that can use the function
datafit and the input data. One way to do it is like this: // Clear windows, memory and screen // Load our functions into memory // Measured data in vectors x and y // Plot the original data // Prepare vector z with given coordinates // copt is supposed to be the best result // Let's see how good our
optimization resulted This is the
result: err = 43.654725
It was a nice try, but the error was very high (it should be close to zero) and our result was not good at all. We could manually try
different values in c0,
the starting
point. We can expect Scilab to deliver different results if we enter
different
seeds as starting points... Let’s try a different
approach. We’re going to create a loop
of 10 iterations. We can create a random vector for c0 (the seed)
each time, and we are
going to take the best result after those 10 attempts. It’s another way
of
approaching the problem, instead of going one vector at a time... I can suggest something
similar to this code... // Let’s try random starting seeds between
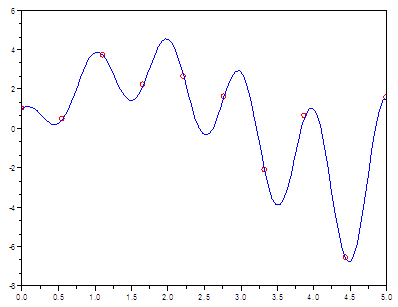
-5 and 5 // The least error after 10 trials is // Let’s plot the best found
result And we get this result... k = 3
Much better..., now our
function has an error of only 0.003
(found in the third iteration) and the best found coefficients produce
a
function that hits the experimental data almost perfectly. Mission accomplished! From 'Curve Fit' to Matlab home From 'Curve Fit' to Scilab examples
|