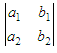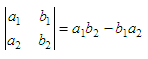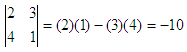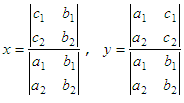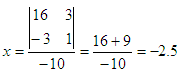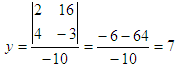Determinants in Matlab

The determinant (in linear algebra) is a value associated with a square matrix, that is a matrix with as many rows as columns. It can be calculated from the elements of the matrix by a specific arithmetic expression. The determinant provides important information in many types of problems, for example, when the matrix represent the coefficients of a system of linear equations... 

The symbol

which consists of the four numbers a₁, b₁, a₂, b₂ arranged in two rows and two columns is called a determinant of second order or of order two. The four numbers are called its elements. By definition,

Then,

Here, the elements 2 and 3 are in the first row, and the elements 4 and 1 are in the second row. Elements 2 and 4 are in column one, and elements 3 and 1 are column two.

The method of solution of linear equations by determinants is called the Cramer’s Rule. A system of two linear equations in two unknowns may be solved using a second order det. Given the system of equations 

it is possible to obtain

These values for x and y may be written in terms of second order dets, as follows:

Example: 

2x + 3y = 16
4x + y = -3

The denominator for both x and y is

Then

and

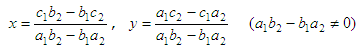
In Matlab, a determinant can be calculated with the built-in function 'det()'.

Using the same numbers as in the example above,

if A = [2 3; 4 1], then det(A) = -10;
if B = [16 3; -3 1], then x = det(A)/det(B) = -2.5;
if C = [2 16; 4 -3], then y = det(C)/det(A) = 7

Naturally, you can use the function det() to find determinants of higher order.  

Cramer's Rule  Simultaneous equations

From 'determinants' to home

From 'determinants' to 'Linear Algebra'