Equation
of a straight line - online calculator
Below
you can use a calculator prepared to find the equation of a straight
line. A line
in a Euclidean space of dimension n
is the set of the points whose coordinates satisfy a given set of n−1 independent linear equations.
|
|
A
line segment is a part of a line that is bounded by two different end
points and contains every point on the line between its end points.
In
analytic geometry, lines in a Cartesian plane can be described
algebraically by linear equations and linear functions. In two
dimensions, the characteristic equation is often given by the
slope-intercept form: |
|
y = mx
+ b
where:
m is the slope of the line
b is the y-intercept of the line
x is the independent variable of the
function y
= f(x) |
 |
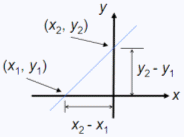The slope
of the line through points (x1,
y1) and (x2,
y2)
is given by
m = (y2 – y1)/(x2
– x1), and the equation of this line
can be written
y = m(x – x1)
+ y2
(notice that b
= y2).
This calculator has three sections: a) you enter two points, and the
calculator returns slope (m)
and intersect (b);
b) you enter slope (m)
and one point (x,
y),
and the calculator returns intersect (b); c) you enter
slope (m)
and one value (either x
or y), and
the calculator interpolates to deliver two points, both (value, y) and (x, value).
Example
1 - You know two points; calculate the slope and the y-intercept:
If you
know two points that are on your line, the calculator returns m and b.
For points (0, 1) and (0.25, 0), you fill in the blanks
Point
1 = (0 1)
Point
2 = (0.25 0)
and you
get
m =
-4.0000
b = 1.0000
Example
2 - You know the slope and the y-intercept; calculate any two points on
the line:
If you
know the slope and the y-intercept,
you can obtain the value of the function at any x or y-value. For a
given m = -4 and b
= 1, you can enter value = 1 (which means in this case both x = 1
and y = 1), like this:
m
= -4
b = 1
value =
1
and you
get points (x, y), first when x = value, and then when y = value.
(value,
y) = (1.0000, -3.0000)
(x,
value) = (0.0000, 1.0000)
From
'Equation of a straight line' to home
From 'Equation of a straight
line' to Free Online Calculators
|
|
