Find Intersections - an engineering approach

The problem of how to find intersections of given lines is very common in math or basic algebra. 

You can find in this site some articles on how to solve linear systems or nonlinear systems, from a more numerical point of view. 

In this article, we’re going to develop a basic an practical approach using a different technique, naturally employing the available Matlab resources. We’re also going to become aware of inherent inaccuracies of digital systems.

Let’s say that we have functions

y₁ = x + 3 (a straight line) and
y₂ = x² – 4 (a parabola)  

and we want to find their intersections.

First approach. Visualize the functions.

We can get points from those functions and plot them, like this: 

x = -4 : .1 : 4;
y1 = x + 3;
y2 = x.^2 -4; 

plot(x,y1,'b', x,y2,'r')
grid on
title('Intersection')
xlabel('x')
ylabel('y') 

The Matlab figure is:

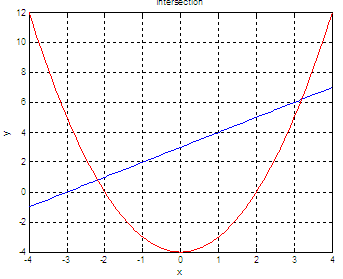
and now we can easily understand how the lines behave and where the intersections are. We can zoom-in the image if needed (use the appropriate icon on the figure menu).

Second approach. Divide element-by-element.

If we need a numerical result and want to find intersections, we can divide one function by the other (element-by-element), and when we get a 1 we know that we’ve found an intersection point. On the practical side, however, we must be aware that our lines are not continuous. We defined x in steps of 0.1 (above). We see a continuous line because Matlab is plotting that, but our vectors are not really continuous (that’s not possible with digital computers).  

A figure that can better display our discrete values is achieved by using 
 

plot(x,y1,'bo', x,y2,'ro')

The resulting figure (showing discrete increments) is: 
 

 
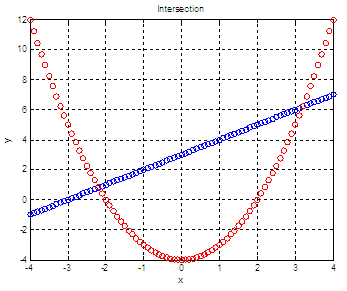
What I mean is that if we divide each element of one function by the corresponding element of the other function, we’re not going to get exactly 1 at the intersections. We may try to find a good approximation if we look for quotients going from 0.95 to 1.05.
 

We may code something like this:
 

d = y1 ./ (y2 + eps);
ix = find(d > .95 & d < 1.05);
x_sol = x(ix)
y1_sol = y1(ix)
y2_sol = y2(ix) 

 
We addd an ‘eps’ to the y2 (in the first line) to avoid a division by zero. ‘eps’ is a predefinded constant and is the smallest number that we can have in Matlab.  

The results are: 
 

x_sol =     -2.2000    3.2000
y1_sol =     0.8000    6.2000
y2_sol =     0.8400    6.2400
 

Note that y1 and y2 are not exactly the same, but close. 

Third approach. Subtract element-by-element.

Another approach to find intersections is to subtract the corresponding elements of the functions. Naturally, we’re not going to find exact zeros at the intersections. We can try, for example, differences of +/- 0.1. Let’s try this code: 

s = y1 - y2;
ix = find(s > -.1 & s < .1);
x_sol = x(ix)
y1_sol = y1(ix)
y2_sol = y2(ix)
 

The results are:
 

x_sol =     -2.2000    3.2000
y1_sol =     0.8000    6.2000
y2_sol =     0.8400    6.2400 

Now, if we need more accuracy, we could start by defining a more continuous x-vector. Instead of 0.1 increments, we might use 0.001 increments, and we could improve our 'specs' or tighten the closeness to 1 for the division of functions, and the closeness to 0 for their subtraction. 

Now, find intersections with Polar coordinates

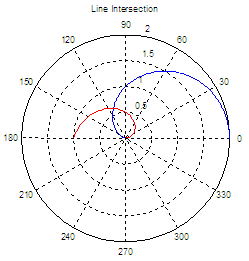
Explore the following code. We use a subtraction between lines, point-by-point. When we find a difference very close to zero, we assume it's an intersection because those two points are the same. This is not an accurate concept, but a practical idea.
 

clear, clc 

% define your angle
t = 0 : 0.001 : pi; 

% define your functions
r1 = 1 + cos(t);
r2 = t/pi; 

% plot
polar(t, r1,'b')
hold on
polar(t, r2, 'r')
title('Line Intersection')
 

% Intersection occurs when r1 - r2 = 0
% Since your function is not continuous,
% your result is an approximation
r = r1 - r2;

% find appropriate or best indices
ix = find(r > -.001 & r < .001); 

% show results
disp('Magnitude aprox: ')
rho1 = r1(ix)
rho2 = r2(ix)

disp('Intersection aprox. at: ' )
radians = t(ix)
degrees = t(ix)*180/pi
 

The results are: 

Magnitude aprox:
rho1 =     0.6233    0.6224
rho2 =     0.6229    0.6233 

Intersection aprox. at:
radians =     1.9570    1.9580
degrees =   112.1278  112.1851 

There’s only one solution, we know. But since we’re finding differences between -0.001 and 0.001, more ‘results’ are possible. From the numerical point of view, those results are the same.