

Geometric mean and geometric deviationThis program computes the geometric mean and geometric deviation of a set of data. We obtain the results in two ways, using iterations and available vectorized operations in Matlab. The geom. mean is given by this formula 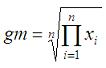 The geom. deviation is given by this formula 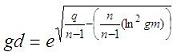 where q is a sum including the natural logarithms of the elements in the set. 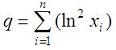 We can use iterations to calculate what we need. In Matlab, this is not the most efficient way to do it, but we can implement the same algorithm in other languages... function [gm, gd] = geo_mean_dev(x) % Take into account the number of elements in the vector n = length(x); % Initialize some variables gm = 1; q = 0; % Iterate through all of the elements for i = 1 : n d = x(i); % Compute mean gm = gm * d^(1/n); % Accumulate intermediate term for deviation q = q + log(d)^2; end % Compute deviation gd = abs(exp(sqrt(q/(n-1)-(n/(n-1)*(log(gm))^2)))); We can test our function as follows (from the command window or from another script): x = [3 5 8 3 7 2]; [gm1, gd1]= geo_mean_dev(x) Matlab response is gm1 = 4.1407 gd1 = 1.7237 We can also use the vectorized form to make it easier and faster... (note that the 'log' function performs the natural logarithm of a number, while the 'log10' function performs the log in base 10) n = length(x); % The 'prod' function gets the multiplication of all the elements gm2 = prod(x)^(1/n) % The 'sum' function gets the sum of the vector q = sum(log(x).^2); % and now we can imlement the last formula gd2 = exp(sqrt(q/(n-1)-(n/(n-1)*log(gm2)^2))) Again, Matlab response is gm2 = 4.1407 gd2 = 1.7237 From 'Geometric Mean' to home From 'Geometric Mean' to 'Matlab Cookbook'
|

