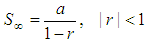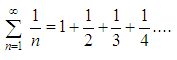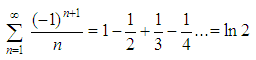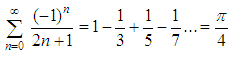Infinite
Geometric and Harmonic Series - working
with numerical software
|
In
this article we
are going to experiment on geometric
and harmonic series.
I
suggest you read the
article Sequences and
Series before reading
this one, to understand the basics...
An infinite geometric
series is an infinite series whose
successive terms have a common ratio. Such a series converges if and
only if
the absolute value of the common ratio is less than one.
|
The sum to
infinity (S∞) of
any geometric
sequence in which the common
ratio r is numerically less than 1
is
given by
where
a
= first number of the series
r
= common ratio
Example
Consider the infinite
geometric series
1 – 1/2 + 1/4 – 1/8 +
1/16...
Then, a = 1 and r = -1/2
So, using the formula
above the sum to infinity is
S = 1/(1-(-1/2)) = 2/3
For the series
1 – 1/3 + 1/9 – 1/27 +
1/81...
a = 1 and r = -1/3
Then, the sum to infinity
is
S = 1/(1-(-1/3)) = 3/4
Let’s experiment with
Matlab.
%
define your first 5 n-elements
n = 0 :
4
%
generate your sequence
s =
(-1).^n ./ 2.^n
%
find its sum
s_to_i
=
sum(s)
The response is:
n
=
0
1
2
3
4
s
=
1.0000
-0.5000
0.2500
-0.1250
0.0625
s_to_i =
0.6875
this shows that five
elements are not giving us enough
precision (0.6875 instead of 0.6667, as we expect). Let’s try more
terms.
%
use 101 elements
format
long
n
= 0 :
100;
s =
(-1).^n ./ 2.^n;
s_to_i =
sum(s)
The answer is
s_to_i =
0.66666666666667, which is much better.
Obviously, we cannot
directly compute a sum to infinity (it
would take too long, right?) but we’re showing that using more terms we
may
reach an approximation as good as we need.
Harmonic Series
A harmonic sequence is a
sequence of numbers whose
reciprocals form an arithmetic sequence. Then 1/2, 1/4, 1/6, 1/8... is
a
harmonic sequence because 2, 4, 6, 8... is an arithmetic sequence.
The harmonic series is
its
name derives from the
concept of overtones, or harmonics
in music.
Even though higher terms
in the sequence are smaller in
value, the series diverges. Let’s explore the series with our numerical
software:
%
define the first 4 terms
n
= 1 :
4
seq =
1./n
%
find the sum of these terms
sum(seq)
The answer is:
n =
1
2
3
4
seq
=
1.0000
0.5000
0.3333
0.2500
ans
=
2.0833
%
define the first 100 terms
n = 1 :
100;
seq =
1./n;
%
find the sume of thes terms
sum(seq)
The answer is:
ans =
5.1874
Alternating Series
The series
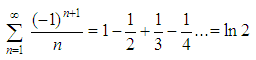
is known as the
alternating
harmonic series. In particular,
the sum is equal to the natural logarithm of 2.
%
our goal
L =
log(2)
%
we try 5 terms
n = 1 :
5
%
define the alternating sequence
seq =
(-1).^(n+1) ./ n
%
get the sum
s
=
sum(seq)
The Matlab answer is:
L =
0.6931
n =
1
2
3
4
5
seq =
1.0000
-0.5000
0.3333
-0.2500
0.2000
s =
0.7833
We see that 5 terms are
not enough. Let’s try 1000 terms.
%
we try 1000 terms
n = 1 :
1000;
%
define the alternating sequence
seq = (-1).^(n+1)
./ n;
%
get the sum
s =
sum(seq)
The new answer is:
s =
0.6926
This is a closer answer,
but we’re still far from log 2.
More terms are needed for higher accuracy... be aware...
Formula for pi
A related series can be
derived from the Taylor series:
This series starts with n
= 0, and it’s known as the Leibniz
formula for pi. Let’s try it in Matlab.
format long
%
goal
p4 =
pi/4
%
we try 1000000 terms to find pi/4
n = 0 :
1000000;
%
define the sequence
seq = (-1).^n
./ (2*n + 1);
%
get the sum
s
=
sum(seq)
The answer is:
p4 =
0.78539816339745
s =
0.78539841339719
We see that with
one-million terms in our series, we only
get 6 decimals right! The series converges very slowly...
Another approach to find pi,
using iterations, just for
fun...
%
What we’re trying to get is
%
(4/1)-(4/3)+(4/5)-(4/7)...
format long
%
You start with 0
calc_pi
= 0;
%
Take the first 100 terms
for n = 0 :
100
% Implement the appropriate
sequence
t = (-1)^n/(2*n + 1);
%
Add-up the terms to try to get pi/4
calc_pi = calc_pi + t;
% Save the values to be
plotted
cp(n+1) = 4*calc_pi;
end
%
Plot the evolution of the algorithm
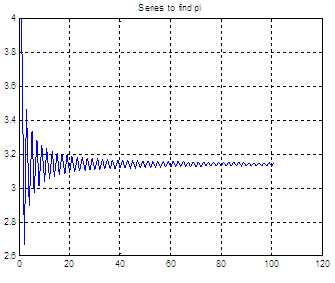
plot(cp)
title('Series
to find pi');
grid on
%
Display the last value found
cp(end)
The result for the calculated pi with 100 terms is:
ans = 3.15149340107099
This is how the series
evolves. It starts with 4 and slowly
tends to 3.14, but after 100 terms it has only reached
3.1514...
From
'Harmonic Series ' to
home
From
'Harmonic
Series ' to Calculus Problems


|