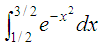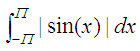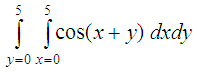Integral Calculator using Scilab

We can use Scilab as a definite integral calculator. The numerical integration of functions in one dimension can be performed with intg(a, b, f) and it’s very easy to use. First, we define the function to integrate...

  
In this example, we define it in a single line, but it can also be defined by writing a separate file and uploading it. Second, we call intg with the limits of the integral. If the function has other arguments besides the variable of integration, you can use a list. This definite integral: 

Can be calculated in Scilab, like this, in two lines:

function y = f(x), y = exp(-x^2), endfunction
I = intg(1/2, 3/2, f)  

and the answer is I = 0.3949074

 
Notice that we can define the function to be integrated in just one line, if the function is simple. We can also use the function deff for the definition of the function, like this:

deff('y = f(x)', 'y = exp(-x^2)') 

Integration with Matlab

If we happen to need the integration of this other function, where we have to calculate the absolute value of the sine function, from –pi to pi radians

we can calculate it like this

function y = f1(x), y = abs(sin(x)), endfunction
I = intg(-%pi, %pi, f1)

and the answer is I = 4 

There are specialized functions to integrate 2D and 3D. As usual, the best reference for the syntax and examples is the online help. Just type  "help" (or "help function" without quotes) on your command window.
 

Function int2d uses an adaptive algorithm in which if a function is rapidly changing, it is divided into finer grids and the integral is recalculated until a convergence is achieved. These type of algorithms are included in many of Scilab’s (or Scicoslab’s) built-in functions such as intg or integrate.

 
For example, the function int2d performs definite two-dimensional integrals by the quadrature and cubature methods. The calling sequence is 

[I, err] = int2d(X, Y, f [,params])

The region of integration is determined by a series of triangles whose vertices are passed through two matrices (X and Y). These vectors have dimension 3xN, where N is the number of triangles and indicates each coordinate of the vertices of the triangles.  

The following example computes the integrand over the two triangles with coordinates (0, 0), (5, 5), (5, 0) and (0, 0), (0, 5) and (5, 5). This describes the rectangle from (0, 0) to (5, 5) and parallel lines to the axes.

X = [0 0; 5 5; 5 0];
Y = [0 0; 0 5; 5 5];
function z = f(x, y), z = cos(x + y), endfunction
[I, error] = int2d(X, Y, f) 

 
the result is 

error = 1.078D-09
I = 0.4063959