Least Squares Fit

Curve Fit in Scilab / Scicoslab

The goal of this article is to provide a simple demonstration of the use of the ‘leastsq’ function in Scilab, which is used to solve nonlinear least squares problems. 

Let’s say that initially we have some measured data points and that we know the form of the function that we should be getting, but we don’t know the coefficients involved. We can develop a simple and practical approach for the fit using the least squares fit function provided in Scilab.

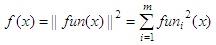which is the sum of the squares of the components of fun. Bound constraints may be imposed on x. 

Let’s suppose that this is our measured information.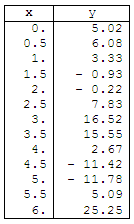  

 
And let’s say that we know that those points are of this form 

and the problem is to find the right coefficients.
 

We can create a file named 'nonlinear_fit_1.sci' with the following two functions, one (fun2fit) to calculate the function and another (myerror) to work on the error to be reduced:

// This is the function to be approximated.
// The error function calls this function iteratively
function y = fun2fit(x, c)
  y =  c(1)*x .* cos(c(2)*x) + c(3);
endfunction 

// This is how we define the error to be minimized.
// Function leastsq iterates through this error until it's
// not posible to reduce it any more.
function e = myerror(c, x, y)
  e = fun2fit(x, c) - y;
endfunction 

Now, we are going to develop the main script which is going to launch the optimization function.
 

// Delete figures, memory and screen
xdel(winsid()); clear; clc 

// Declare the objective function, or function to be minimized
getf('nonlinear_fit_1.sci') 

// Define our initial data or measured points
x = [ 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6]';
y = [5.02  6.08  3.33 -0.93   -0.22  7.83 ...
    16.52 15.55  2.67 -11.42 -11.78  5.09 25.25]';   

// This is our guessed coefficients. First attempt.
c0 = [1 1 1]';
y0 = fun2fit(x, c0); 

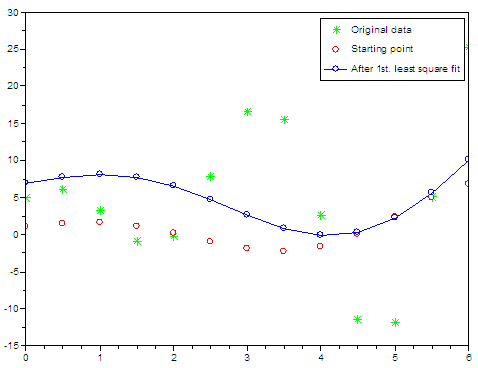
// Plot the original points and the starting point in our problem
set("current_figure", 0)
plot(x, y, 'g*', x, y0, 'ro') 

// Launch the optimization function. Provide data and coefficients
[f, copt] = leastsq(list(myerror, x, y), c0) 

// Plot results after optimization
yopt0 = fun2fit(x, copt);
plot(x, yopt0, 'bo-')
legend(['Original data'; 'Starting point'; 'After 1st. least square fit']);
 

This is the comparison of the different situations in our problem.

The solution provided by the least-squares fit is 

copt  =
    1.8023481
    0.8337166
    6.9000138 

 f  =
    1148.0038
 

The function result (f) is a very large number. It should be as close to zero as possible.

 
Since the solution is not good at all, we need to change the starting point and try different coefficients. Everything is the same but the starting point.
 

// This is our guessed coefficients. Second attempt.
c0 = [1 2 3]';
y0 = fun2fit(x, c0); 

set("current_figure", 1)
plot(x, y, 'g*', x, y0, 'ro') 

[f, copt] = leastsq(list(myerror, x, y), c0)
yopt0 = fun2fit(x, copt);
plot(x, yopt0, 'bo-')
legend(['Original data'; 'Starting point'; 'After 2nd. least square fit']);
 

This is the comparison of the different situations in our problem, in our second experiment.

The new results are: 

copt  =
    4.000196
    1.9999978
    4.9992435 

 f  =
    0.0011237 

The function is close enough to zero and now the solution is what we needed. We have found the coefficients in our problem.