Recursion or self-calling routine

1.- Basics

Example of recursive code:

function y = ten_exp(n)
% This is a recursive program for computing y = 10^n.
% The program works only if n is a nonnegative integer.
% If n is negative, the algorithm won't stop. 

if n == 0
    y = 1
else
    n  %<< this line is not needed but for inspection
    y = 10 * ten_exp(n-1)
end
 

Semicolons were avoided in those statements (on purpose) to see the value updates in different levels of the recursion. You can explore the code by running the step-by-step feature while at the editor.

This code has a construction using a branch. The comparison n == 0 is the base of the recursion, because it defines the final step or lowest level. This is the only way to get the program to stop calling itself.

The ‘else’ part in the branch is the key to recursivity. The trick is that it is calling a lower value (n - 1), and it will continue to do so until it gets down to n = 0.

 
There are several considerations while using this self-calling technique:

• The first is that it is possible for the function to call itself forever and never return an answer. That happens in the code above if we enter a negative argument.

• The second is that recursion can lead to redundant calculations which can be time consuming. The code above uses instructions again and again that could be performed using a single line of code (10^n).

• The third consideration is that it needs more memory allocation. In calculations on large systems, memory space should not be wasted on program overhead.

 
On the other hand, recursive programs can be easier to write and read than nonrecursive programs. 

2.- Recursivity to solve Factorials

Now, we’re going to write a function to compute a factorial (n!) using this technique, again. We know that it’s not the most efficient way to compute a factorial number, but it is conceptually a recursive calculation easy to test and implement...
 

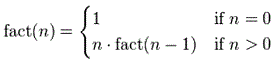
function y = fact(n)
% We have the highest number
y = n 

% We go down to 0
if n == 0
    y = 1  
else
    % We multiply by all the integers before ours,
    % one at a time...
    y = y * fact(n-1)
end 

Again, these are the considerations for this example:

• It is possible for the function to call itself forever and never return an answer. That happens in the code above if we enter a negative argument.

• There are redundant calculations which can be time consuming. The code above uses instructions again and again that could be performed using a single built-in function (factorial(n)). 

3.- Video: Puzzle solved with Recursivity