Scilab Functions

 
So far, we've written relatively short programs, but now that we've learned the basics of Scilab, we're ready to write longer codes. In this short article, I’m gonna show you some techniques that will allow us to write longer (and wiser) programs with a minimum of extra time and effort.  

We'll show you how to declare sripts and functions and how to use them in your programs. You'll also learn how the Scilab environment is designed for modular programming. By the end of this article, you'll have all the tools you need to write compact, well organized codes. 
 

Why Scripts (or procedures or modules)?  

Notice that a single program can contain a section that is repeated over and over without modification. Such repetitive task not only takes time and effort to type in but also clutters up the program listing, making it more difficult to work with. Is there an easier way to code a program that has repetitive parts or sections?  

The answer is yes! Scilab provides a programming structure called script that lets you type a block of statements, assign a name to it, and then call it by name whenever you want your program to execute it.  

Scripts and functions (procedures) provide the following advantages:  

• Scripts eliminate repeated lines. You can define a procedure once and have your program execute it any number of times.
• Scripts make programs easier to read. A program divided into a collection or group of smaller parts is easier to take apart and understand. 
• They simplify program development. Programs separated into logical units are easier to design, write, and debug. Plus, if you're writing a program along with anyone in the world, you can exchange functions or single algorithms instead of entire programs.
• They can be reused in other programs. You can incorporate your general-purpose scritps into other programming projects.
• Scripts and functions extend the Scilab language. They can often perform tasks that can't be accomplished directly by built-in Scilab statements or functions.  

In this article you'll learn to create and use two Scilab procedures: scripts and functions. Scripts let you subdivide your program into smaller units that can be called one or more times. Functions return values that the rest of your program can use.  

Creating Scripts   

Scripts (which in older programming languages were called subprograms), make your code easy to read and reduce repetition. A script is a block of code between the “function” and “endfunction”  statements. You can have your program call a script as often as you like. When a script or function end, control returns to the statement that follows the subprogram call in the main program. In Scilab, you create and store scripts/functions separately from the main code or program.  
 

Syntax of a Script  

The syntax of a script is as follows:  

function name(parameter list) 
      local variable and constant declarations 
      statements 
endfunction 
 

• “function” is the Scilab statement that marks the beginning of the subprogram definition.
• “name” is the name of the script. It’s the name that the main program uses to call the subprogram. It can't be a Scilab keyword or be the same as any variable name or procedure name in your program.
• “parameter list” is an optional list of input variables.
• “local variable and constant declarations” is an optional list of variables and constants used within the script. They have no effect on variables or constants with the same name elsewhere in the program.
• “statements” is the working part of the subprogram. You can use any Scilab statements in a script.
• “endfunction” is the Scilab statement that marks the end of the script definition.  

Syntax of a Function  

The syntax of a function in Scilab is as follows:  

function [output list] = name(input list) 
      local variable and constant declarations 
      statements 
endfunction 
 

A function can return one or more values to the calling module. That’s the main difference with the scripts.  
 

Calling a Subprogram (script or function)  

After you have created and declared a script/function, you can call (execute) it. To call a module, simply specify the subprogram name (along with any arguments the function requires) in the body of the main program or another calling script.

A script or function is a Miniprogram  

Think of a script or function in Scilab as a small, self-contained subprogram. A subprograrn should complete an important task in a program and yet be general enough to be used in other programming projects.  

The following tasks are often best suited to subprograms:

• Getting input from the user
• Displaying information on the screen
• Processing several numeric values or strings
• Drawing shapes or plots
• Returning multiple values to the calling module
• Performing numeric calculations and returns of string values
• Generating random numbers
• Converting one value to another
• Evaluating a logical expression and returning a value of true or false
• Calculating one result from several arguments
• The Main Program Handles Declaration and Control  

What tasks are left for the main program to handle?  

Actually, not many if you make thorough use of scripts and functions. The following tasks are often best suited to the main program:

• Introductory comments and explanations
• Initialization of key variables and structures
• Program code that is executed only once
• Flow-control structures that determine the path of program execution

The following declarations must be included in the main program if they appear in a program:

• Global variable declarations
• Scripts and function declarations  

Now that you've learned about the main program, subprograms, and functions, you're ready to start writing well-organized and modular programs.
 

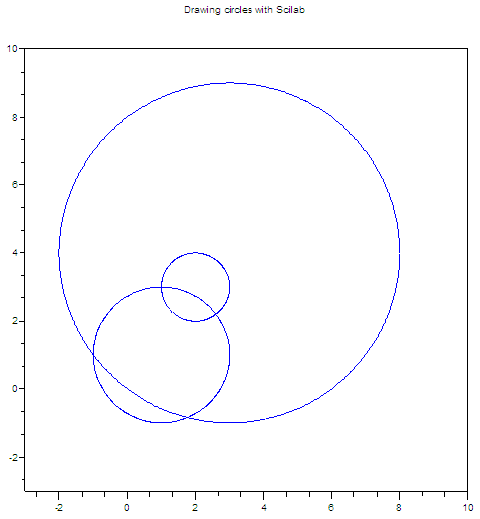
Example 

We’ll draw some circles with Scilab. We’ll first define a script whose input parameters are the x and y-values of the center, and the radius.  

We’ll later use this script from the main code.
 

// We start with the word function, then the name and input
// variables
function drawcircle(xc, yc, r)
  // xc = x-value of the center
  // yc = y-value of the center
  // r = radius of the circle 

  // We find horizontal and vertical values of a parametric 
  // circle
  t = 0 : .01 : 2*%pi;
  x = xc + r * cos(t);
  y = yc + r * sin(t); 

  // We now plot the x and y-values
  plot(x, y) 

// We end our function with this sentence
endfunction 

Now, we execute the main program:
 

// We need to load in memory all of the functions to be used
getf('drawcircle.sci') 

// We execute the script once
drawcircle(3, 4, 5) 

// We add a title to our plot
title('Drawing circles with Scilab') 

// This sentence keeps the same plot without deleting data.
// It's more or less equivalent to the Matlab's hold on
set(gca(),"auto_clear","off") 

// Now we execute the same function with different 
// centers and radii
drawcircle(1, 1, 2)
drawcircle(2, 3, 1) 

// We have to adjust the axes to keep a square proportion
square(-3, -3, 10, 10)
 

The result is as follows: