Singular
Value Decomposition (SVD)
|
Let's suppose that a matrix A
is singular. Then, let A
be a real m
x n matrix
of rank r,
with m greater
than or equal to n. The Singular
Value Decomposition (svd)
of A
is
A
= U
S V'
(the apostrophe after a matrix or vector means its transpose) where U
is an orthogonal m x n matrix, S is an r x r diagonal matrix, and V is
an n x n square orthogonal matrix. |
Since U
and V
are orthogonal, then
UU'
= I
and VV'
= I
That
is, the transpose
of each matrix is equal to its inverse.
The elements along
the diagonal of S,
labelled  ,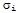
are called the singular
values of A.
There are r
such singular values and they
satisfy
If the
matrix A
is square, then we can use the singular value decomposition to find
the inverse, which is is
A-1
= (USV')-1
= (V')-1S-1U-1
= VS-1U'
since
(AB)-1
= B-1A-1, UU'
= I,
and VV'
= I.
If A
is a square matrix then
And so,
If an
SVD of a matrix A
can be calculated, so can be its inverse. Therefore, we can
find a solution to a system
Ax
= b
=> x
= A-1b
= VS-1U'b
that
would otherwise be usolvable.
Example:
Let's
find with Matlab the singular value decomposition of
A = [ 0
-1
-2 1
1 0]
We simply type:
[U,S,V]
= svd(A)
and the
above operation produces a diagonal matrix S,
of the same dimension as A
and
with nonnegative diagonal elements in decreasing order, and unitary
matrices U
and V
so that A
= U*S*V'.
The Matlab
answer is:
U =
-0.1826
-0.8944 0.4082
0.9129
0.0000 0.4082
-0.3651
0.4472 0.8165
S =
2.4495
0
0 1.0000
0
0
V =
-0.8944 0.4472
0.4472
0.8944
>>
We can
confirm the values of UU',
VV'
and USV,
by executing these instructions in
Matlab
U*U'
V*V'
U*S*V
The confirming
responses are:
ans =
1.0000
-0.0000 -0.0000
-0.0000
1.0000 -0.0000
-0.0000
-0.0000 1.0000
ans =
1 0
0 1
ans =
-0.0000 -1.0000
-2.0000 1.0000
1.0000
0.0000
From
'Singular Value Decomposition' to home
From
'Singular
Value Decomposition' to 'Linear Algebra'
|
